|
|
Вычисление доверительного интервала и доверительной вероятностиМы уже убедились в том, что именно из-за наличия случайных погрешностей отдельные значения измеряемой величины х1, х2, х3, … хi в большинстве случаев оказываются неодинаковыми, и в качестве наилучшего значения искомой величины выбирается среднее арифметическое из n измерений: Значение случайной ошибки Δх чаще всего оценивается с помощью стандартной, или средней квадратичной ошибки (ее часто называют сокращенно стандартом измерения). Средней квадратичной ошибкой (погрешностью) называется величина
где n – число измерений. Если число измерений n очень велико, то подверженная случайным колебаниям величина Sn стремится к некоторому постоянному значению σ, которое называется статистическим пределом Sn : σ = Доверительный интервал Δх при небольшом числе измерений n и соответствующая ему доверительная вероятность σ связаны соотношением Это соотношение было выведено Стьюдентом в предположении, что вероятности случайных отсчетов распределены по нормальному закону, для которого плотность вероятности р(Δхi) задается Гауссовой кривой (рис. 13). Величина α характеризует «ширину» кривой, то есть степень разброса величины хi относительно 0: чем меньше σ, тем выше точность измерения. По мере уменьшения σ рассеяние случайных погрешностей относительно центра их распределения (относительно
Рис. 13. Гауссовы кривые
Из рис. 13 видно, что вероятность численно равна площади S заштрихованной фигуры, ограниченной функцией р(Δхi),отрезком оси погрешностей Δхi от -Δr до Δr и ординатами р(-Δr), р(Δr).Чем шире заданный интервал погрешностей (-Δr, Δr), тем больше площадь S,то есть выше вероятность попадания случайных погрешностей измерений Δ в этот интервал. Для интервала погрешностей (-∞, ∞) вероятность Р(-∞ < Δ < ∞) = 1. Таблица 4 Коэффициенты Стьюдента
Пользуясь таблицей коэффициентов Стьюдента, можно решать две задачи: 1) находить доверительный интервал Δх при заданной вероятности α и известном числе измерений n. Для этого из таблицы коэффициентов Стьюдента находим значение tαn для заданных α и n, а затем определяем доверительный интервал по формуле: 2) указывать доверительную вероятность вычисленной погрешности измерений при определенном числе измерений. Для этого нужно вычислить значение коэффициента Стьюдента по формуле Проиллюстрируем примером деятельность по решению задачи № 1. Пример. Обработка результатов наблюдений при сличениях масс[7]. В результате сличения меры массы 1 кг с эталонной мерой массы того же номинала получена группа результатов наблюдений, приведенных в первом столбце следующей таблицы. Во втором столбце 2 приведены значения xi0 = (хi - 999,998000)·106, в третьем и четвертом столбцах – результаты вспомогательных расчетов.
Измерение выполнено методами точного взвешивания, исключающими погрешность от неравноплечности весов. Таким образом, систематические погрешности при измерении можно считать отсутствующими. О случайных погрешностях на основании ранее накопленных данных известно, что их распределение можно принимать за нормальное. Измеряемую массу полагаем равной среднему арифметическому, найденному по формуле `х = 999,998000 + `xio = 999,998721 г. Далее вычисляем по известной формуле и данным четвертого столбца оценку среднего квадратического отклонения наблюдений:
Теперь можно найти доверительную погрешность результата. Возьмем α = 0,95 и, пользуясь распределением Стьюдента, находим коэффициент t = 2,26. Случайная погрешность составит Δm = 2,26·5·10-6 = 11·10-6 г. Таким образом, масса m исследуемой меры лежит в интервале 999,998710 г £ m £ 999,998732 г. Более компактная запись полученного результата имеет вид m0,95 = 999,998721 ± 11·10-6 г.
|
|
 . В теории вероятности это среднее арифметическое называют наиболее вероятным значением измеряемой величины, или выборочным средним.
. В теории вероятности это среднее арифметическое называют наиболее вероятным значением измеряемой величины, или выборочным средним. =
=  =
= 
 . Собственно говоря, именно этот предел и называют средней квадратичной ошибкой. В действительности, однако, мы всегда вычисляем не величину σ, а ее приближенное значение Sn, которое тем ближе к σ, чем больше n.
. Собственно говоря, именно этот предел и называют средней квадратичной ошибкой. В действительности, однако, мы всегда вычисляем не величину σ, а ее приближенное значение Sn, которое тем ближе к σ, чем больше n. где
где  – коэффициенты Стьюдента[5], значения которых приведены в таблице 4.
– коэффициенты Стьюдента[5], значения которых приведены в таблице 4. ) уменьшается[6].
) уменьшается[6].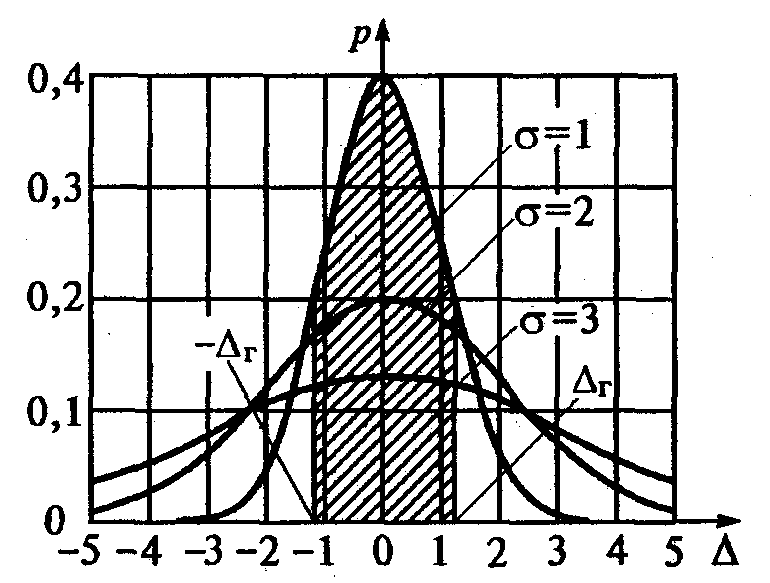

 а затем подобрать подходящее значение α из таблицы коэффициентов Стьюдента при известном числе измерений n.
а затем подобрать подходящее значение α из таблицы коэффициентов Стьюдента при известном числе измерений n.