|
|
Кинематика поступательного и вращательного движений.МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ Федеральное государственное образовательное учреждение Высшего профессионального образования «Орловский государственный аграрный университет» Кафедра физики МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ПО КУРСУ ФИЗИКИ Часть I
Орел, 2007. Методические указания предназначены для студентов очной и заочной форм обучения Орловского государственного аграрного университета, изучающих курс физики по программе инженерных дисциплин.
Указания составлены в соответствии с ГОСТ и рабочими программами по физике специальностей 110301, 110302, 110304, 280102, 270102, 270115, 250203. Рецензенты: д.т.н., зав. кафедрой «Математика» Орел ГАУ Моисеенко А.М. ст. преподаватель кафедры «Физика» Орел ГАУ Тверская Н.В.
В подготовке методических указаний принимали участие Гладких Ю.В., Ставчикова Л.Ф., Васильева В.В., Зубова И.И. Ответственные за выпуск Гладких Ю.В., Васильева В.В.
Издание второе, дополненное и переработанное.
Обсуждено на заседании кафедры физики, протокол №7от «30» марта 2007г.
Методические указания одобрены методической комиссией факультета гуманитарных и естественнонаучных дисциплин, протокол №9от «14» мая 2007г. и методическим советом ОрелГАУ, протокол №10 от 28 июня 2007г.
© Гладких Ю.В., Ставчикова Л.Ф., Васильева В.В., Зубова И.И. © Издательство Орел ГАУ Методические указания к решению задач. Решение физических задач следует проводить в определенной последовательности и соблюдая ряд указанных ниже требований. 1. Выписать данные задачи в колонку в принятом стандартном буквенном обозначении. Если необходимо обозначить несколько сходных величин, можно ввести большие и малые буквы или индексы (например, различные сопротивления в электрической цепи можно обозначить R1, R2, R3, r и т.д.) 2. Величины, приведенные в условиях задачи, выразить в одной системе единиц, наиболее подходящей для данной задачи (предпочтительно в СИ). 3. Вспомнить физические законы, на основании которых следует производить решение задачи. Дать формулировку этих законов. Написать соответствующие им формулы. 4. Если это необходимо, сделать схематический чертеж (рисунок, график, схему), поясняющий содержание задачи. Например, изобразить тело с приложенными к нему силами, график изменения объема газа при нагревании, схему электрической цепи, ход лучей в оптических системах и т.д. 5. Решение задачи сопровождать краткими пояснениями. 6. Решение большинства задач сводится к составлению алгебраических уравнений, отражающих заданный физический процесс. Поэтому задачи необходимо доводить до конца не в числовом, а в буквенном виде. При таком способе ответ получается в виде формулы, которая позволяет проверить полученный результат, а промежуточные выкладки дают возможность проверить любую часть решения и исключить ошибки. Ответ, полученный в общем виде, позволяет сделать анализ решения, тогда как числовой отпет сделать это не дает возможности. 7. Получив ответ в виде алгебраической формулы, следует проверить его на основании правил размерностей, то есть убедиться, что размерности правой и левой частей равенства совпадают. 8. Проверив совпадение размерностей, следует произвести анализ полученного ответа и выяснить, удовлетворяет ли он условиям задачи. Так, при решении квадратного уравнения получаются два ответа, один из которых может не удовлетворять данным задачи и его следует отбросить. 9. Произведя проверку, можно подставить в полученную формулу числовые значения величин, приведенных в условиях задачи. При арифметических подсчетах следует использовать правила приближенных вычислений и производить расчеты лишь с тем количеством значащих цифр, которое определяется условиями задачи. Если правило размерностей было проверено, то подставлять наименования в расчетную формулу не следует, так как это лишь загромождает расчеты. В окончательном результате наименование полученной величины записывается в СИ. 10. Записать ответ. Пример решения задачи. Вал в виде сплошного цилиндра массой m1 = 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m2 = 2 кг. С каким ускорением а будет опускаться гиря, если ее предоставить самой себе?
Линейное ускорение а гири равно тангенциальному ускорению точек вала, лежащих на его цилиндрической поверхности, и связано с угловым ускорением ε вала соотношением a=rε, где r – радиус вала. Угловое ускорение вала выражается уравнением динамики вращающегося тела ε=M/J, где М – вращающий момент , действующий на вал; J – момент инерции вала. Рассматриваем вал как однородный цилиндр. Тогда его момент относительно геометрической оси равен J=1/2m1r2. Вращающий момент М, действующий на вал, равен произведению силы натяжения Т шнура на радиус вала: М=Tr. Силу натяжения шнура найдем из следующих соображений. На гирю действуют две силы: сила тяжести m2g, направленная вниз, и сила натяжения Т шнура, направленная вверх. Равнодействующая этих сил вызывает равноускоренное движение гири. По второму закону Ньютона, m2g - T=m2a, откуда T=rn2(g-a). Таким образом, вращательный момент M=m2(g-a)r.
Ответ: а = 2,8 м/с2 Кинематика поступательного и вращательного движений. Скорость прямолинейного движения в общем случае ускорения:
Ускорение:
В случае прямолинейного равномерного движения:
В случае прямолинейного равномерного движения:
В этих уравнениях ускорение а положительно при равноускоренном движении и отрицательно при равнозамедленном.
При вращательном движении в общем случае угловая скорость:
Угловое ускорение:
В случае равномерного вращательного движения угловая скорость равна:
В случае равнопеременного вращательного движения:
где t – период обращения, v – частота обращения, т.е. число оборотов в единицу времени.
Угловая скорость w связана с линейной скоростью v соотношением:
Тангенциальное и нормальное ускорение при вращательном движении могут быть выражены следующим образом:
где at – тангенциальное ускорение, an – нормальное (центростремительное) ускорение, причем:
где v – скорость движения, R – радиус кривизны траектории в данной точке.
Задачи. 1. Зависимость пройденного телом пути S от времени t дается уравнением S=A-Bt+Ct2, где А=6 м, В=3 м/с и С=2 м/с2. Найти среднюю скорость и среднее ускорение тела в интервале времени от 1 с до 4 с. Построить график пути, скорости и ускорения для 0<t<5 через 1 секунду. 2. Зависимость пройденного телом пути S от времени t дается уравнением S=A+Bt+Ct2, где А=3 м, В=2 м/с и С=1 м/с. Найти среднюю скорость и среднее ускорение тела за первую, вторую и третью секунды его движения. 3. Мяч бросили со скоростью v=10 м/с под углом α=40о к горизонту. Найти: 1) на какую высоту Sy поднимается мяч, 2) на каком расстоянии Sx от места бросания мяч упадет на землю, 3) сколько времени он будет в движении. Сопротивление воздуха не учитывать. 4. Ось с двумя дисками, расположенными на расстоянии l=0.5 м друг от друга, вращается с угловой скоростью, соответствующей частоте v=1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; при этом отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол f=12°. Найти скорость пули. 5. Найти радиус вращающегося колеса, если известно, что линейная скорость v1 точки, лежащей на ободе, в 2.5 раза больше линейной скорости v2 точки, лежащей на 5 см ближе к оси колеса. 6. Вал вращается с постоянной скоростью, соответствующей частоте 180 об/мин. С некоторого момента вал тормозится и вращается равнозамедленно с угловым ускорением, численно равным 3 рад/сек2. 1) Через сколько времени вал остановится? 2) Сколько оборотов он сделает до остановки? 7. Колесо вращается с постоянным угловым ускорением ε=2 рад/сек2. Через t=0.5 сек после начала движения полное ускорение колеса стало равно а=13.6 см/сек2. Найти радиус колеса. 8. Эскалатор метро поднимает неподвижно стоящего на нем пассажира за 1,5 мин. По неподвижному эскалатору пассажир мог бы подняться за 6 мин. Сколько времени затратит пассажир, если будет подниматься по движущемуся эскалатору? 9. Мимо пристани проходит плот. В этот момент в поселок, находящийся на расстоянии 15 км от пристани, вниз по реке отправляется моторная лодка. Она дошла до поселка за время 3/4 ч и: повернув обратно, встретила плот на расстоянии 9 км от поселка. Каковы скорость течения реки и скорость лодки относительно воды? 10. Свободно падающее тело проходит последние 50 м за 0,5 с. Определите высоту падения тела. Ускорение свободного падения 10 м/с2. 11. Точка движется по окружности с постоянной скоростью 50 м/с. Вектор скорости изменяет направление на 30° за время 2 с. Каково нормальное ускорение точки? По дороге со скоростью 70 км/ч едут две автомашины: грузовая и за ней легковая. С заднего колеса грузовой автомашины срывается камень. На каком расстоянии должна держаться легковая автомашина, чтобы камень не мог попасть в нее? |
|


 Подставив в формулу (2) полученные выражения М и J, найдем угловое ускорение вала:
Подставив в формулу (2) полученные выражения М и J, найдем угловое ускорение вала: Для определения линейного ускорения гири подставим это выражение ε в формулу (1). Получим:
Для определения линейного ускорения гири подставим это выражение ε в формулу (1). Получим: откуда
откуда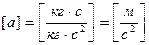







 ,
,



