Тело, двигаясь равноускоренно, за пятую секунду от начала движения проходит 45 м. Определить модуль перемещения тела за 5 с и его скорость в конце пятой секунды. Начальная скорость тела равна нулю.

28. На горе с углом наклона α к горизонту бросают мяч с начальной скоростью v₀ перпендикулярно склону горы (см. рис.). Найти время полета мяча. На каком расстоянии от точки бросания упадет мяч?

29. Небольшое тело скользит со скоростью v = 10 м/с по горизонтальной плоскости, приближаясь к щели. Щель образована двумя отвесными параллельными стенками, находящимися на расстоянии d = 0,05 м друг от друга. Глубина щели H = 1 м . Сколько раз ударится тело о стенки, прежде чем упадет на дно? Удар о стенку абсолютно упругий (т.е. при ударе модуль скорости не меняется и угол отражения равен углу падения).

30. Какое расстояние по горизонтали пролетит мяч, брошенный со скоростью v = 10 м/с под углом α = 60° к горизонту, если он ударится о потолок? Высота потолка h = 3 м, удар упругий. Сопротивлением воздуха пренебречь.

31. Число зубьев одной из шестерен зубчатой передачи Z₁ = 18, а второй Z₂ = 90. Определить угловую скорость второй шестерни, если первая совершает n₁ = 3000 об/мин.

32. Гладкий диск радиусом R, плоскость которого горизонтальна, вращается вокруг своей оси с частотой n =40 об/мин . От поверхности диска на расстоянии R/2 от оси отрывается небольшое тело, которое без трения скользит по диску. Через какое время оно соскользнет с диска?

33. Диск начинает движение из состояния покоя и вращается равномерно-ускоренно. Каким будет угол между векторами скорости и ускорения произвольной точки диска, когда он сделает k оборотов?

34. С самолета, летящего горизонтально со скоростью v₀ = 720 км/ч, отделяется тело. Найти центростремительное и тангенциальное ускорение тела, а также радиус кривизны траектории движения тела в точке, которую оно достигает через τ = 5 с после начала движения. Сопротивлением воздуха пренебречь.

35. Точка двигалась в течение t₁ = 15с со скоростью v₁ = 5м/с, в течение t₂ = 10 c со скоростью v₂ = 8м/с и в течение t₃ = 6с со скоростью v₃ = 20м/с. Определить среднюю путевую скорость (v) точки.

36. Три четверти своего пути автомобиль прошел со скоростью v₁ = 60 км/ч, остальную часть пути — со скоростью v₂ = 80 км/ч. Какова средняя путевая скорость (v) автомобиля?

37. Первую половину пути тело двигалось со скоростью v₁ = 2 м/с, вторую — со скоростью v₂ = 8 м/с. Определить среднюю путевую скорость (v).

38. Тело прошло первую половину пути за время t₁ = 2 с, вторую — за время t₂ = 8 с. Определить среднюю путевую скорость (v) тела, если длина пути S = 20м.

39. Уравнение прямолинейного движения имеет вид х = At + Bt², где А = З м/с, В = - 0,25м/с². Построить графики зависимости координаты и пути от времени для заданного движения.

40. Движение материальной точки задано уравнением х = At + Bt², где А = 4м/с, В = - 0,05м/с². Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени.

41. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением a = 0,1м/с², человек начал идти в том же направлении со скоростью v = 1,5м/с. Через какое время t поезд догонит человека? Определить скорость v₁ поезда в этот момент и путь, пройденный за это время человеком.

42. Камень падает с высоты h = 1200м. Какой путь s пройдет камень за последнюю секунду своего падения?

43. Камень брошен вертикально вверх с начальной скоростью v₀ = 20м/с. По истечении какого времени камень будет находиться на высоте h = 15м? Найти скорость v камня на этой высоте. Сопротивлением воздуха пренебречь. Принять g = 10м/с².

44. С балкона бросили мячик вертикально вверх с начальной скоростью v₀ = 5 м/с. Через t = 2 с мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю.

45. Точка движется по кривой с постоянным тангенциальным ускорением а_τ = 0,5м/с². Определить полное ускорение а точки на участке кривой с радиусом кривизны R = Зм, если точка движется на этом участке со скоростью v =2 м/с.

46. За время t = 6 с точка прошла путь, равный половине длины окружности радиусом R = 0,8 м. Определить среднюю путевую скорость (v) за это время и модуль вектора средней скорости |(v)|.

47. С вышки бросили камень в горизонтальном направлении. Через промежуток времени t = 2 с камень упал на землю на расстоянии s = 40 м от основания вышки. Определить начальную v₀ и конечную v скорости камня.

48. Самолет, летевший на высоте h = 2940м со скоростью v = 360 км/ч, сбросил бомбу. За какое время t до прохождения над целью и на каком расстоянии s от нее должен самолет сбросить бомбу, чтобы попасть в цель? Сопротивлением воздуха пренебречь.

49. Тело брошено под некоторым углом α к горизонту. Найти этот угол, если горизонтальная дальность s полета тела в четыре раза больше максимальной высоты Н траектории.

50. Линейная скорость v₁ точек на окружности вращающегося диска равна 3 м/с. Точки, расположенные на ΔR = 10см ближе к оси, имеют линейную скорость v₂ = 2м/с. Определить частоту вращения n диска.

51. На цилиндр, который может вращаться вокруг горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t = 3 с опустился на h = 1,5м. Определить угловое ускорение ε цилиндра, если его радиус r = 4см.

52. Диск радиусом r = 10см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением ε = 0,5 рад/с². Найти тангенциальное a_τ, нормальное а_п и полное а ускорения точек на окружности диска в конце второй секунды после начала вращения.

53. Маховик начал вращаться равноускоренно и за промежуток времени Δt = 10с достиг частоты вращения n = 300 мин^-1. Определить угловое ускорение ε маховика и число N оборотов, которое он сделал за это время.

54. Велосипедное колесо вращается с частотой n = 5 с ^-1.Под действием сил трения оно остановилось через интервал времени Δt = 1 мин. Определить угловое ускорение ε и число N оборотов которое сделает колесо за это время.

55. Диск вращается с угловым ускорением ε = -2рад/с² Сколько оборотов N сделает диск при изменении частоты вращения от п₁ = 240 мин ^-1 до n₂ = 90 мин ^-1?.Найти время Δt, в течение которого это произойдёт.

2. Динамика поступательного движения материальной точки.

Уравнение движения материальной точки (второй закон Ньютона):

или

где - геометрическая сумма всех сил, действующих на материальную точку.

Сила упругости:

где k – коэффициент упругости; х – абсолютная деформация.

Сила гравитационного воздействия:

γ= 6,67·10^-11 Нм²/кг² – гравитационная постоянная.

Сила трения:

где f – коэффициент трения.

Закон сохранения импульса:

Закон изменения импульса:

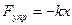
Задачи.

1. Два груза массой m₁ и m₂, связанные между собой с помощью невесомой и нерастяжимой нитью, движутся в горизонтальном направлении по гладкому столу под действием силы F, приложенной к первому грузу (рис.). Определить ускорение грузов и силу натяжения нити.

2. По горизонтальной поверхности может скользить тело массой m=1 кг под действием силы F, направленной под углом α=30^о к горизонту (рис.). Коэффициент трения между телом и поверхностью μ=0,1. Определить силу трения и ускорение тела при F=1 Н и F=2 Н.