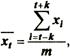Тема 21: Прогнозирование социальных процессов

Прогнозирование в социологии — это способ научного предвидения с той или иной степенью вероятности итога, направленности, или характера протекания социальных процессов в течение некоторого промежутка времени.

Момент времени, на который в распоряжении социолога имеются исходные данные социаль­ной статистики (результатов исследования), и до момента, к которому относится прогноз, называ­ется периодом упреждения. Максимальная величина периода упреждения в прикладной социоло­гии не превышает нескольких месяцев. Более длительный прогноз имеет очень низкую достовер­ность из-за того, что социальные процессы в течение времени подвержены воздействию большого числа факторов.

Главная особенность прогнозирования — нацеленность на будущее и попытка преодолеть неопределенность, обусловленную отсутствием знаний о точном значении статистических параметров характеристик социальных процессов. Любой прогноз в при­кладной социологии носит только вероятностный характер, то есть предсказание является досто­верным с той или иной степенью вероятности. Отсюда следует, что для любой обоснованной прогностической модели необходимы два критерия:

1. Форма числовой оценки характеристик социальных явлений.

2. Степень погрешности оценки, её точность.

Форма оценки изменения числовых параметров характеристик социального явления на тот или иной период упреждения зависит от вида шкалы измерения, на основе которой строится прогностическая модель.

На величину погрешности прогноза влияет количество факторов, воздействующих, с той или иной степенью "интенсивности", на вариацию характеристик социального процесса в течение периода упреждения.

Ряд требований к любой прогностической модели. Эти требования: обоснованность, полнота, валидность, точность и устойчивость,

Под обоснованностью прогностической модели понимается её соответствие цели прогноза на весь период упреждения.

Полнота прогностической модели зависит от объема, достоверности и устойчивости исходной социальной статистики.

Валидность прогностической модели – это ее способность учитывать изменение структурных элементов именно прогнозируемого явления.

Точность прогностической модели – это ее способность давать количественную оценку параметров изучаемого процесса на период упреждения, минимально отличающуюся от их фактического значения.

Устойчивость прогностической модели заключается в ее способности быть валидной на весь период упреждения.

По методам в прикладной социологии различают три вида прогноза: 1) аналогия; 2) экспертиза; 3) статистический прогноз.

Аналогия – это метод исторического соотнесения двух или более идентичных явлений, порожденных схожими социальными обстоятельствами в разные временные периоды.

Экспертная оценка как метод прогнозирования является способом аккумуляции научных знаний и практического опыта профессионалов по вопросам, имеющим непосредственное отношение к предмету прогноза.

Два этих метода наименее точны, однако применимы для долгосрочных прогнозов.

Статистические методы прогнозирования основаны на формулах и приемах математической статистики, однако пригодны в социологии для краткосрочного прогнозирования (до одного года).

Прогнозируемая динамика ряда распределения количественных параметров исследуемого социального процесса состоит из взаимосвязанных компонент: тренда, интервала циклов и тенденции.

Тенденция – это направление развития социального процесса.

Тенденция, механизм реализации которой функционально зависит от времени, называется трендом.

Одна из важнейших математических процедур, предшествующих прогнозированию, проверка гипотезы о наличии или отсутствии тренда.

Методы определения наличия тренда:

1. Метод разности средних уровней. Этот метод предполагает разбиение объекта исследования на две подвыборочные совокупности, идентичные по основным контролируемым параметрам. Для каждой из совокупностей вычисляется средняя по показателю, после чего определяется разность значений средних. Если расхождение существенное, то тренд имеет место. Если незначительное, то его можно приписать воздействию случайных факторов и гипотеза о наличие тренда отвергается.

t – статистика для проверки гипотезы о наличии тренда вычисляется по формуле: _ _

t = x₁ – x₂ / σ,

_ _

где: x₁ и x – средние соответственно первой и второй подвыборочной совокупностей;

σ – среднее квадратическое отклонение разности средних.

Для определения истинности гипотезы о тренде вычисленное значение t сравнивается с таб­личным значением t_p (р — вероятность ошибки). При t ≥ t_p гипотеза о наличии тренда подтвержда­ется, а при t < t_p — отвергается.

Значение t_p берется с числом степеней свободы, равным n₁ + n₂ - 2, где n₁ и n₂объемы подвыборочных совокупностей соответственно.

Среднее квадратичное отклонение (σ) определяется по формуле:

(n₁ - 1)² σ₁² + (n₂ - 1)² σ₂² 1 1

σ = -------------------------------- * ----- + -----

n₁ + n₂ – 2 n₁ n₂

где σ₁² и σ₂² — дисперсии подвыборочных совокупностей соответственно.

Приведенные формулы дают достаточно истинные значения t-статистики для проверки гипо­тезы о наличии тренда в том случае, если значения дисперсий изучаемого признака в обеих подвыборочных совокупностях достаточно близки. Проверка однородности дисперсий реализуется с помощью t-критерия Фишера:

σ₁²

F = ----- , (при σ₁² >σ₂² )

σ₂²

Значение рассчитанного при помощи приведенной формулы критерия сравнивается с его таб­личным значением. Если расчётное значение F меньше табличного, то гипотеза о статистическом равенстве дисперсий принимается. Если расчётное значение F больше его табличного значения, то гипотеза о равенстве дисперсий отклоняется, а это означает, что вышеприведенные формулы не могут быть применены для проверки гипотезы о наличии тренда изучаемого социального про­цесса. Данные формулы достаточно точны для малых и менее точны для больших выборочных совокупностей.

3. Метод среднего темпа роста. Средний темп роста можно получить как геометрическую среднюю ряда последовательных тем­пов роста. Последовательный темп роста характеризует отношение како­го-либо уровня динамического ряда к предыдущему уровню и выражается в процентах или в долях единицы. В последнем случае его называют коэффициентом роста. Если ряд состоит из числовых уровней x₁, х₂, ..., х_n , то последовательные темпы будут равны:

х₂ х₃ х_n

q₂ = -----, q₃ = ----- ,…, q_n = ------

x₁ х₂ х_n-1

Последовательные темпы прироста, выраженные в долях единицы, исчисляются из соотноше­ния p_n = q_n - 1.

Если темп прироста устойчивый, то для вычислений можно использовать средний темп роста:

q_n

q = ^n-1 q_1* q_2*…* q_n = ^n-1 ----

q₁

Для получения значений, являющих собой минимальный набор для про­гнозирования, необходимо провести не менее трех повторных исследований, числовые данные которых полностью сопоставимы.

3. Метод сглаживания динамического ряда. Один из приемов сглаживания вариации заключается в расчете скользящих средних. Применение этого метода в прикладной социологии требует проведения не менее 6 повторных исследований.

Принцип сглаживания следующий. Вычисляется средняя для 2, 3 и т. д. совокупностей уров­ней. Предпочтительно брать в совокупностях нечетное число уровней. Скользящая средняя для i-й совокупности рассчитывается по формуле:

где: x — значение скользящей средней на момент t = 1, 2, ..., i, ... р;

х₁ — фактическое числовое значение уровня на момент i;I;

i — порядковый номер уровня в интервале сглаживания;

m — число уровней в интервале сглаживания.

Величина k определяется по формуле:

m - 1

k = --------, (при нечетном m)

Регрессионный анализ. Для уравнения регрессии определяют доверительные интервалы. Их расчет позволяет определить область, в которой следует ожидать значение прогнозируемой величины. При помощи регрессионного уравнения измеряют степень зависимости контролируемого признака от факторных. Регрессионный анализ позволяет строить прогностические модели и осуществлять теоретический эксперимент.

Регрессионный анализ предполагает решение двух задач:

1) выбор взаимно независимых (факторных) переменных, влияющих на вариацию значений исследу­емого показателя и определение формы уравнения регрессии; 2) оценку параметров при помощи того или иного статистического метода обработки первичной социологической информации.

Для оценки параметров регрессий удобно использовать метод наименьших квадратов.

В зависимости от числа признаков, взаимосвязь которых исследуется, регрессия может быть парной или множественной.