|
|
Электролитпен коагуляциялау кинетикасы 1 главаБІРІНШІ ТАРАУ І. КІРІСПЕ 1.1 Коллоитық химияның дамуына қысқаша тарихи шолу. 1.2 Заттың коллоидық күйінің негізгі ерекшеліктері. 1.3 Коллоитық химияның зеріттейтін нысандарының басты белгілері. 1.4 Коллоитық және дисперстік жүйелердің жіктелуі. 1.4.1 Дисперстілік көрсеткіші немесе дисперстік бөлшектердің өлшемі бойынша жіктелуі. 1.4.2 Дисперстік фаза мен дисперсиялық ортаның агрегаттық күйіне байланысты жіктелуі. 1.4.3 Дисперстік фаза мен дисперсиялық ортаның әрекеттесу сипаты немесе дисперстік жүйелердің термодинамикалық тұрақтылығы бойынша жіктелуі. 1.4.4 Дисперстік фазаның бөлшектернің өзара әрекеттесу сипаты немесе дисперстік фазаның кинетикалық қасиеті бойынша жіктелуі. 1.5 Беттік құбылыстардың жіктелуі. БІРІНШІ БӨЛІМ. БЕТТІК ҚҰБЫЛЫСТАР ЕКІНШІ БӨЛІМ. ДИСПЕРСТІК ЖҮЙЕЛЕР А) ЛИОФОБТЫҚ КОЛЛОИТЫҚ ЖҮЙЕЛЕР ЕКІНШІ ТАРАУ 2. КОЛЛОИТЫҚ ЖҮЙЕЛЕРДІҢ ОПТИКАЛЫҚ ҚАСИЕТТЕРІ 2.1 Жарықтың шашырауы (опалесценция) 2.1.1 Опалесценция және флуоресценцция. 2.1.2 Коллоитық жүйедегі шашыраған жарықтың поляризациясы мен индикатриссасы. 2.2 Жарықтың коллоитық жүйеде жұтылуы (абсорбциялануы) 2.3 Коллоитық жүйелерді зерттеудің оптикалық әдістері. 2.3.1 Нефелометірлік әдіс. 2.3.2 Турбидиметриялық әдіс. 2.3.3 Ултрамикроскопиялық әдіс. 2.3.4 Электрондық микроскопиялық әдіс. 2.3.5 Рентген сәулелері мен электрондардың дифракциясына негізделген әдістер. 2.4 Коллоитық жүйелердің түстері, металдық кірнелердің оптикалық қасиеттерінің ерекшеліктері. 2.5 Сәуленің коллоитық жүйелерде қосарлана сынуы. ҮШІНШІ ТАРАУ 3. ДИСПЕРСТІК ЖҮЙЕЛЕРДІҢ МОЛЕКУЛАЛЫ-КИНЕТИКАЛЫҚ ҚАСИЕТТЕРІ 3.1 броундық қозғалыс 3.2 Коллоитық жүйелердегі диффузия. 3.3 Коллоитық жүйелердегі осмостық құбылыс. 3.4 Доннанның мембраналық тепе-теңдігі. 3.5 Седиментация. Седиментациялық – диффузиялық тепе – теңдік. 3.6 Дисперстік жүйелерді седиментациялық талдау. 3.6.1 Иін таразысы арқылы седиментациялық талдау жүргізу. 3.6.2 Фигуровскийдің таразысы арқылы седиментациялық талдау жүргізу. 3.6.3 Седиментация қисықтары және оларды өңдеу. 3.7 Коллоитық бөлшектердің шамасын анықтау әдістері. 3.7.1 Ультрасүзгіштік (ультрафильтрациялық) әдіс. 3.7.2 Седиментациялық (шөгу) әдісі. 3.7.3 Ультрацентрифугалық әдіс. 3.7.4 Диффузиялық әдіс. ТӨРТІНШІ ТАРАУ 4. КОЛЛОИДТЫҚ ЖҮЙЕЛЕРДІҢ ЭЛЕКТІРЛІК ҚАСИЕТТЕРІ 4.1 Электркинетикалық құбылыстар . 4.2 Электркапиллярлық құбылыстар. 4.2.1 Электркапиллярлық қисықтық теңдеуі және оны экспримент түрінде зерттеу. 4.2.2 БАЗ- дың электркапиллярлық қисыққа әсері. 4.3 Қос электрлік қабаттың пайда болуы. 4.3.1 Иондарға ыдырау нәтижесінде зарядтардың пайда болуы. 4.3.2 Зарядтардың адсорбция нәтижесінде пайда болуы. 4.4 Қос электірлік қабаттың құрлысы. 4.4.1 Гельмгольц – Пеерен теориясы. 4.4.2 Гүй – Чепмен теориясы. 4.4.3 Штерн теориясы. 4.5 Электркинетикалық потенциялға әртүрлі факторлардың әсерлері. 4.5.1 Индифферентік электролиттердің әсерлері. 4.5.2 Индифферентік емес электролиттердің әсерлері. 4.5.3 Орнатың рН – ның әсері. 4.5.4 Коллоидтың жүйенің концентрациясының әсері. 4.5.5 Температураның әсері. 4.5.6 Дисперсиялық ортаның табиғатының әсері. 4.6 Лиофобтық коллоидтық мицелланың құрлысы. 4.7 Электрофорез және электросмос құбылыстарын сандық түрде сипаттау. Гельмгольц – Смолуховский теңдеуі. Ә) ЛИОФИЛЬДІК КОЛЛОИДТЫҚ ЖҮЙЕЛЕР 1. КОЛЛОИДТЫҚ БЕТТІ - АКТИВТІК ЗАТТАР 1. Коллоидтық бетті-активтік заттар туралы түсінік 2. Коллоидтық БАЗ –дар: жіктелуі, негізгі сипаттамалары, алынуы және қолданылуы. 2.А Коллоидтық БАЗ –дардың жіктелуі 2.Ә Коллоидтық БАЗ –дардың негізгі сипаттамалары, алынуы және қолданылуы. 2.1 Аниондық БАЗ 2.2 Катиондық БАЗ 2.3 Иондық емес БАЗ 2.4 Цвиттер – иондық БАЗ 3. Коллоидтық БАЗ – дың негізгі ерекшеліктері 3.1 Коллоидтық БАЗ – дың беттік активтілігі 3.2 ГЛБ туралы түсінік, БАЗ – дың әсер ету механизімі бойынша жіктелуі. 4. БАЗ – дың мицелла түзуі. МТДК – ға әртүрлі факторлардың әсерлері. 4.1 МТДК – ға БАЗ – дың молекулалар құрылысының әсері. 4.2 МТДК – ға еріген заттардың және температураның әсері. 4.3 БАЗ ерігіштігінің температураға тәуелділігі. Крафт құбылысы. 5. Мицеллатүзілудің қозғаушы күштері және термодинамикалық модельдері. 5.1 Гидрофобтық әрекеттесулер. 5.2 Фазалық бөлу моделі. 5.3 Массалар әрекеттесу заңына негізделген модель. 5.4 Көптеген тепе – теңдіктер моделі. 6. БАЗ ертінділеріндегі солюбилизация. 7. БАЗ – дың дисперстік жүйеге тұрақтандырғыштық әсері. 8. Мицелла түзілудің кризистік концентрациясын анықтау әдістері. 9. БАЗ – дарды анықтау әдістері. 10. Коллоидтық БАЗ ертінділернің практикалық маңызы. 11. БАЗ – дың дерматологиялық әсері. 12. БАЗ – дың қошаған ортаға әсері. 12.1 Су қоймаларына қатысты уландырғыштық. 12.2 Биоыдырау жылдамдығы және БАЗ молекулаларның құрлымы. 12.3 Қоршаған ортаны қорғау – жаңа қауіпсіз БАЗ – ды іздеудің стимулы. 2.ҮЛКЕН МОЛЕКУЛАЛЫҚ ҚОСЫЛЫСТАР (ҮМҚ) ЕРІТІНДІЛЕРІНІҢ ҚАСИЕТТЕРІ 2.1 ҮМҚ классификациясы 2.2 ҮМҚ-ның еріткішпен әрекеттесуі 2.3 ҮМҚ ерітінділерінің қасиетттері 2.3.1 ҮМҚ-дың ерітінділерінің термодинамикалық қасиеттері 2.3.2 ҮМҚ-дың ерітінділерінің тұтқырлығы 2.4 Полиэлектролитттер 2.5 Тоңазытпалар 2.5.1Тоңазытпа түзілу 2.5.2 Тоңазытпалардың қасиеттері 3.МИКРОГЕНДІК ЖҮЙЕЛЕР Бірінші тарау:Жүзгіндер 1.1 Жүзгіндердің жіктелуі 1.2 Сұйытылған жүзгіндерді алу жолдары 1.3 Сұйытылған жүзгіндердің қасиеттері 1.4 Сұйытылған жүзгіндердің седиментациялық тұрақтылығы 1.5 Сұйытылған жүзгіндердің агрегаттық тұрақтылығы 1.6 Сұйытылған жүзгіндерді бұзу әдістері 1.7 Қойытпақтар 1.8 Дисперсиялық талдау 1.9 Жүзгіндердің қолдану аймақтары Қайталауға және өзін- өзі бақылауға арналған сұрақтар Екінші тарау: Майғындар 2.1 Майғындардың жіктелуі 2.2 Майғындарды алу әдістері 2.3 Майғындардың негізгі сипаттамалары 2.4 Майғындардың агрегаттық тұрақтылығы 2.5 Майғындағыштың түрлері 2.6 Майғындардың типін анықтау 2.7 Майғын фазаларының ауысуы 2.8 Майғындарды бұзу тәсілдері 2.9 Майғындарды практикада қолдану Қайталауға және өзін- өзі бақылауға арналған сұрақтар Үшінші тарау: Көбіктер 3.1 Көбіктің жіктелуі 3.2 Көбіктерді алу әдістері 3.3 Көбіктердің негізгі сипаттамалары 3.4 Көбіктердің қасиеттері 3.5 Көбіктің тұрақтылығы 3.6 Көбіктерді бұзу әдістері 3.7 Көбіктердің практикада қолданылуы Қайталауға және өзін -өзі бақылауға арналған сұрақтар Төртінші тарау: Аэрокірнелер 4.1 Аэрокірнелердің жіктелуі 4.2 Аэрокірнелерді алу әдістері 4.3 Аэрокірнелердің жалпы сипаттамалары 4.4 Аэрокірнелерді бұзу әдістері 4.5 Аэрокірнелік баллондар 4.6 Аэрокірнелердің практикада қолданылуы Қайталауға және өзін- өзі бақылауға арналған сұрақтар Бесінші тарау: Ұнтақтар 5.1 Ұнтақтардың жіктелуі 5.2 Ұнтақтарды алу әдістері 5.3 Ұнтақтардың жалпы сипаттамасы 5.4 Ұнтақтардың қасиеттері 5.5 Ұнтақтардың тұрақтылығы 5.6 Ұнтақтардың практикада қолданылуы Қайталауға және өзін- өзі бақылауға арналған сұрақтар ҚОРШАҒАН ОРТАНЫ ҚОРҒАУДЫҢ КОЛЛОИДТЫ-ХИМИЯЛЫҚ НЕГІЗДЕРІ 1. Дисперсияларды өздігінен және сыртқы күш әсерінен бұзылуы 2. Дисперсияларды бұзудың механикалық әдістері 3. Дисперсияларды бұзу үшін ортокинетикалық гетерокоагуляцияны қолдану А) Микрофлотация және сүзу Ә) Микрофлотацияны ортокинетикалық гетерокоагуляция ретінде қарастыру Б) Сүзуді жанасу коагуляциясы ретінде қарастыру 4. Коагулянттар мен флокулянттарды қолдану 5. Электрлік сүзу 6. Кері осмос және динамикалық жарғақтар 7. Аэрокірнелерді бұзу әдістері Қорытынды Бірінші бөлім МОЛЕКУЛАЛЫҚ ӘРЕКЕТТЕСУ ЖӘНЕ ФАЗАЛАРДЫҢ БӨЛУ БЕТТЕРІНІҢ ЕРЕКШЕ ҚАСИЕТТЕРІ
Барлық денелер өздерін қоршап тұрған ортадан бөліну беттері арқылы бөлінеді. Әрине, егер денелер өте үлкен болса, онда бөліну беттерінің қасиеттері аздап ғана өзгереді. Неғұрлым денелер кішірейген сайын, соғұрлым олардың бөліну беттерінің рөлі күшейе түседі. Дисперленген бөлшектердің беттік ауданының өте көп шама екенін біз коллоидтық жүйелердің ерекше қасиеттерін қарастырғанда айтқанбыз. Сондықтан да коллоидтық жүйелерде беттік ауданның әсерінің шешуші мәні бар.
Беттік керілу
Сұйықтықтардағы беттік керілуді қарастырайық. Егер сұйықтықтың молекуласы сол сұйықтықтың көлем ішінде болса, онда оған жан-жағындағы молекулардың бірдей әрекеттесуінің әсерінен шешуші күш 0-ге тең болады. /1.1а-сурет/.

1.1. - сурет. Молекулалық күштер
Ал егер қарастырып отырған молекуламыз бөліну бетінен өзінің әсер ететін радиусының мөлшерінен аз қашықтықта болса, онда молекулаға жан-жақтан әсер ететін күш әртүрлі болғандықтан, олар толық /компенсацияланбайды/ теңелмейді де, стрелкамен көрсеткендей шешуші күш пайда болады. /1.1ә сурет/. Ол күш молекуланы беттен сол көлем ішіне қарай тартуға тырысады. Бұл күштің ең жоғары мәні молекула бетте болғанда ғана болады. /1.1б сурет/. Қарастырылып отырған күшті ішкі, иә молекулалық күш деп атайды. Кейде, молекулалық қысым деп те атайды. Молекулалық қысымның мәні заттың полярлығы өскен сайын жоғары болады. Өйткені бұл қысымның негізгі себебі молекулалардың арасында болатын күштің әсерінен болады. Мысалы: Судың ішкі қысымы – 14800 атм, ал бензолдікі – 3800 атм. Сонымен сұйықтықтардың ішкі қысымы бетте тұрған молекуланы көлем ішіне қарай тартып, қарастырылып отырған жаңағы сұйықтықтың беттік ауданан азайтуға тырысады. Бөлу бетінің 1 өлшем ұзындығына әсер етіп, сұйықтықтың беттік ауданын азайтатын күшті – беттік керілу күші, немесе жай беттік керілу деп атайды. Оның өлшем бірлігі дин /см, ал ӨЖ (СИ) жүйесінде н/м болады. Бұл күш әрқашанда бетке перпендикуляр бағыттылған. Егер, молекуланы көлем ішінен бетке шығаратын болсақ, онда бетті көбейту үшін ішкі қысымды жеңетіндей жұмыс істеу керек. Ыдыс ішінде белгілі бір S беттік ауданы бар сұйықтықты қарастырайық. /1.2а сурет/.
1.2. - сурет. Беттік керілу
Ыдысты қисайту арқылы сол сұйықтықтың бетін арттыруға болады. Әрине ол үшін көлемнен молекулалардың белгілі бір санын бетке шығару керек. Ендеше шыққан молекулалардың саны сол жаңадан пайда болған бетке пропорционал. Сонымен, біз ыдысты қисайта отырып, ыдыстың ауырлық орталығын өзгертетін механикалық жұмыстан басқа, бетті арттыратын жұмыс та істедік. Қайтымды және изотермиялық үдеріс үшін, бірлік бетті құратын жұмыс сол беттің меншікті еркін энергиясына тең. Меншікті еркін энергияның өлшем бірлігі - эрг/см2, ӨЖ (СИ) бойынша дин/м2. Эрг/см2=дин/см тең екенін еске алсақ, меншікті еркін энергия деп отырғанымыз беттік керілу екенін түсіну қиын емес. Беттік керілуді σ символымен белгіленеді. Ендеше: Сонымен, беттік энергияның қарқындылық факторы беттік керілу екен (F=S*σ). Ол фазааралық молекулааралық күштердің теңгерілмеген (компенсацияланбаған) өрісінің нәтижесінде болатынын білдік. Енді беттік керілудің термодинамикалық анықтамасына тоқталайық. σ-дің термодинамикалық анықтамасы термодинамиканың І және ІІ заңдарының біріктірілген теңдеуінен де шығады. Гетерогендік жүйелер үшін:
Мұндағы: Sэ-энтропия, V-көлем, p-қысым, µi-і компонентінің (құрамдасының) химиялық потенциалы; ni-і құрамдасының моль саны; φ-потенциал; q-заряд. Егер бұл теңдеуден S, V, n, q – тұрақты болса, онда олардың дифференциалы 0-ге тең, ендеше,
Термодинамиканың І және ІІ заңдарының біріктірілген теңдеуін басқа да термодинамикалық потенциалдарға да ( H, F және G) жазуға болады, ендеше олардан:
Сонымен, σ кез келген термодинамикалық потенциалдардың фазааралық беттік ауданы бойынша дербес дифференциалы екен. Әдетте, Р мен Т –ны эксперимент арқылы оңай тұрақты етуге болатындықтан:
жиі қолданылады, бұдан σ мен µі ұқсастығын көреміз. Олардың біріншісі-термодинамикалық потенциалдың беттік ауданы,ал екіншісі- заттың мольі бойынша дербес дифференциалы екен. Сонымен, беттік керілуді жұмыс (энергия) ретінде де және күш ретінде де қарастыруға болады екен. Бірінші жағдайда оның өлшем бірлігі ӨЖ (СИ) жүйесі бойынша Дж/м2 , ал СГС жүйесі бойынша –эрг/см2 . Ал күш ретінде қарастырғанда оның өлшем бірлігі ӨЖ (СИ) жүйесі бойынша н/м, ал СГС жүйесі бойынша дин/см және осы өлшем бірліктердің арасындағы қатынастар былай болады:
1Дж/м2 =1000 эрг/см2=1н/м=1000 дин/см. Төменде кейбір заттардың бөлмелік температурадағы беттік керілуінің мәні 10-3 Дж/м2 өлшем бірлігі бойынша берілген:
Табиғатта барлық үдерістердің, егер сыртқы күш әсер етпесе, өзбетінше жүйенің энергиясын азайтатынын білеміз. Мысалы:қисық жазықтықтағы шарды алып қарасақ, ол төмен құлайды. Өйткені, онда оның энергиясы өте аз. Біз жоғарыда айтылған мысалда беттің өсуі, яғни энергияның артуы өзбетінше болмайтындығын айтып кеткен жөн. Өйткені сұйықтықтың беті, сол беттің өсуіне кедергі болатын қабыршық тәрізді болады. Сондықтан сұйықтық әрқашанда беті өте аз шама болатындай пішін алуға тырысады. Мысалы: Су тамшысы шар тәрізді болады. Өйткені шар-заттың ең кіші бет түзетін пішіні. Сонымен, термодинамиканың заңы бойынша кез келген жүйедегі өздігінен жүретін үдерістер сол өзінің энергиясының азаю жағына қарай жүретінін көрдік. Жоғары формуладан (ΔF= σ ∙ ΔS) еркін энергия беттік керілу мен беттік ауданының көбейтіндісіне тең. Ендеше жүйедегі өздігінен жүретін үдерістер, иә беттік керілуді, иә беттік ауданды /екі жағынан қабат болуы да мүмкін/ азайтуға тырысады. Сұйықтықтардың беттік керілуі температурасы өскен сайын азаяды. Бұл температуралық коэффициент
1.3. - сурет. Беттік керілудің
Жеке сұйықтықтар үшін бөлу беті түзілген кезде олардың беттік керілудің мәні өте жылдам, шамамен алғанда 0,001 секундта, қалыптасады. 5.2. Термодинамикалық функциялардың беттік қабаттағы шоғырлануы. Термодинамиканың заңдарына сәйкес конденсирленген жүйелер үшін беттің ішкі энергиясының артық мөлшерін бірлік бетке арнап жазатын болсақ, ол былай болады: Us=Gs+TSs. (16) Мұндағы Us, Gs, және Ss- бірлік бетке сәйкес келетін ішкі энергия, Гиббс энергиясы және энтропия, Т- абсолюттік температура. Термодинамиканың 2-заңына сәйкес. qs=TSs, (17) Мұндағы qs-қайтымды үдерістердегі бірлік бетті жасау жылуы. Таза сұйық үшін s= Gs екендігін еске алатын болсақ, жоғарыдығы теңдеуді қайта былай жаза аламыз: Us=s+qs. (18) Жаңа бет жасау барысында әр уақытта жылу сіңіріледі, яғни qs>0. Олай болса, беттің ішкі энергиясының шамасы Гиббс энергиясының бірлік мәніне бетті жасау барысында сіңірілген жылудың шамасын қосқанға тең. Ішкі энергияны – беттің толық энергиясы деп атайды. Термодинамиканың 1- және 2- заңдарына сәйкес Гиббс энергиясының өзгерісін бірлік бетке арнап жазайық: dGs= - SsdT+Vdp+sdS+åmidni+j*dq (19)
S, p, ni, және q тұрақты болғанда: Ss=(dGs/dT)s, p, n, q (20)
Олай болса (18) теңдеуді (17) және (20) теңдеулерін ескере отырып басқаша былай жазуға болады: Us=s - T(dGs/dT)s, p, n,= s - T(ds/dT) (21) Бұл теңдеу – Гиббс- Гельмгольц теңдеуі деп аталады. Ол беттің толық энергиясының Гиббс энергиясымен, беттік керілумен және температурамен байланысын өрнектейді. Бұл теңдеуге сәйкес, сұйықтардағы беттің толық энергиясынын анықтау үшін оның беттік керілуі мен беттік керілудің температураға тәуелділігін (температуралық коэффициентінің) білу жеткілікті. Көптеген ассоциацияланбаған сұйықтарда температура жоғарылағанда олардың беттік керілулері түзу сызық бойымен төмендейді, яғни ds/dT=const<0 (5,5 сурет) ds/dT= - Ss екендігін еске алсақ, онда температура өскенде таза сұйықтық бірлік бетіне сәйкес келетін энтропиясы өзгеріссіз қалатындығын аңғару қиын емес және көптеген сұйықтар үшін ол 0,1 мДж (м2*К) шамасына жуық келеді. Беттік керілудің температураға тәуелділігін сипаттайтын теңдеуді алу үшін (20) теңдеуді интегралдайық. Ол үшін Т0 температурадағы беттік керілуді s0, ал Т температурадағы беттік керілуді s деп белгілейік. Сонда: (Формула жазу керек)…………. Бұдан s=s0- Ss(T- Т0) (22)
Демек, сұйықтың белгілі бір Т0 температурадағы беттік керілу (s0) мен энтропиясының (Ss) мәндері белгілі болса, онда оның кез- келген температурадағы (дағдарыстың температурадан Тд алшақ жатқан аймақта) беттік керілуін (22) теңдеуі арқылы есептеуге болады. Енді беттің толық энергиясының температураға байланысын қарастырайық. Ол үшін (21) теңдеудің температура бойынша туындысын анықтайық: dUs/dT=ds/dT-ds/dT- Td2s/dT2=- Td2s/dT2. Ассоциацияланбаған таза сұйықтарда ds/dT=const болатындықтан, d2s/dT2=0. Олай болса dUs/dT=0, Us=const (23) (сурет салу).......... Бұдан мынадай қорытынды туындайды: беттің толық энергиясының меншікті ( бірлік бетке сәйкес келетін) мәні температураға тәуелсіз (5,5-сурет). Көрсетілген беттің термодинамикалық параметрлерінің температураға байланысты өзгерістерін дағдарыстың температурадан алшақ жатқан температуралар арлығында ғана орындалады. Өйткені дағдарыстың температура (Тд) маңайында фазааралық бөлу беті жойылады. Сондықтан, дағдарыстың температураға жақындағанда беттің барлық термодинамикалық параметрлері күрт төмендеп, нольге ұмтылады(5,5- сурет).
1.2. Екі сұйықтық арасындағы беттік керілу
Осы жоғарыда айтылғандардың бәрі сұйықтық пен газ аралығындағы сұйықтықтың беттік керілуі туралы еді. Бұл жүйелер үшін сұйықтық пен газдың /иә будың/ арасындағы әрекеттесуі өте аз болғандықтан оларды елеген жоқ болатынбыз. Ал сұйықтық пен сұйықтықтың арасындағы беттік керілуде олардың әрекеттесуін қарастырмауға болмайды. Өйткені 1-сұйықтықтың молекулалары өзінде шамалы еритін екінші сұйықтықтың молекулаларын өздеріне тартып 1-сұйықтықтағы компенсацияланбаған, яғни теңгерілмеген күштердің әсерін азайтады. Екі сұйықтықтың полярлығының айырмашылығы неғұрлым аз болса, соғұрлым беттік керілудің азаюы күшейеді. Егер екі сұйықтық полярлығы жағынан шамалас болса, бір-бірімен өте жақсы араласады да /ериді/ олардың беттік керілуі 0-ге тең болады, яғни оларды бөлетін бөлу беттері болмайды. Ал егер екі сұйықтық бір-бірінде аз еритін болса, онда олардың бөлу беттеріндегі беттік керілу шамасын Г.Н. Антонов ережесі бойынша табуға болады. Өзара шамалы еритін, бір-біріне қаныққан екі сұйықтықтың арасындағы беттік керілу сол сұйықтықтардың ауа арасындағы болатын беттік керілулерінің айырмашылығына тең болатынын 1907 ж. Г.Н. Антонов көрсеткен болатын. Бұны теңдеу түрінде былай жазуға болады: |
|

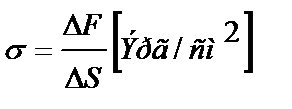
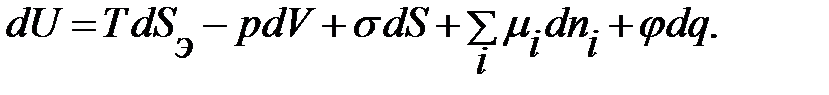
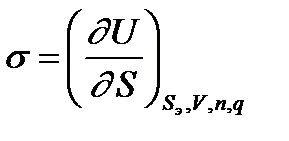
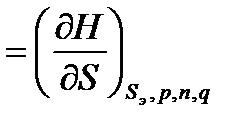
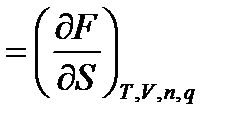
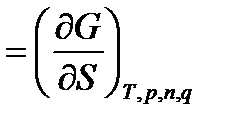
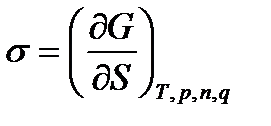
 ылғида жуықтап алғанда тұрақты және теріс шама болғандықтан, σ-ның азаюы түзүсызықты заңдылықта болады: σT=σ0+γT. Әрине, температура дағдарыстық температураға жеткенде σ=0-ге тең болады. Өйткені бұл температурады бөлу беті болмайды. Мысалы, сұйықтық-бу жүйесі үшін, сұйықтықтың қайнау температурасы, ал сұйықтық-сұйықтық жүйесі үшін, сол сұйықтықтардың өзара еритін қасиеті байқалатын температурасы. Д.И. Менделеев бұл температураны дағдарыстық (кризистік) температура деп атаған.
ылғида жуықтап алғанда тұрақты және теріс шама болғандықтан, σ-ның азаюы түзүсызықты заңдылықта болады: σT=σ0+γT. Әрине, температура дағдарыстық температураға жеткенде σ=0-ге тең болады. Өйткені бұл температурады бөлу беті болмайды. Мысалы, сұйықтық-бу жүйесі үшін, сұйықтықтың қайнау температурасы, ал сұйықтық-сұйықтық жүйесі үшін, сол сұйықтықтардың өзара еритін қасиеті байқалатын температурасы. Д.И. Менделеев бұл температураны дағдарыстық (кризистік) температура деп атаған.