|
|
Электролитпен коагуляциялау кинетикасы 4 глава
А Ә Б A=const В
p C=const
28-сурет. Адсорбцияның изотермасы (А), изобарасы (Ә), изостерасы (Б), және изотермадан изостера мен изопикна тұрғызу (В). Температураны тұрақты етіп ұстау да өте оңай, сондықтан изотерма бұл тәжірибе арқылы алынатын , көп таралған тәуелділік.Ал қалған тәуелділіктерді әр түрлі температура табылған графикалық изотермадан тұрғызуға болады.11.6 – суретте нүктелі жүйе изотерманы қиып, ордината осіне параллель изопикнаға сәйкес келеді, ол түзу изотермаларын қиып, абцисса осіне параллель болса, изостераның нүктесі алынады.Алынған нүктелерден адсорбция мәнінің тәуелділігін немесе концентрацияның (изостерасы) температураға тәуелділігін тұрғызады. Изотерма, изопикна, изостераның математикалық байланысын көрсетейік. А мәнінің толық дифференциалы, күй функциясына сәйкес келеді: dA=(dA/dc)Tdc+(dA/dT)CdT А мәнін тұрақты десек, (dA/dc)T(dc)A+(dA/dT)C(dT)A=0 немесе (dA/dc)T (dc/dT)A +(dA/dT)C=0 Соңғы теңдікті (dT/dA) мәніне көбейтсек, (dA/dc)T (dc/dT )A . (dA/dT)C=-1 (11.55) Бұл белгілі математикалық қатынас термодинамикада кең қолданылады.Бұл жағдайда жеке туындылар изотерма, изостера, изопикнаға сәйкес.Ал (11.55) теңдеу олардың дифференциалдық қатынасын береді.Ол арқылы туындылардың әрқайсысын басқалары белгілі болғанда жеке-жеке табуға болады. (сурет салу)................ Ал кейбіреулерін теориялық жолмен қорытуға болмайтындықтан, тәжірибеге негізделген эмпирикалық теңдеулермен көрсетуге болады. (Мысалы Фрейндлихтің изотермасының теңдеуі). Адсорбцияны мынадай жалпы белгілермен сипаттауға болады. 1. Термодинамикалық қайтымдылығымен яғни адсорбцияға қарама-қарсы үдеріс десорбцияның динамикалық тепе-теңдігімен: адсорбция 2. Үдерістің экзотермиялығымен, яғни адсорбция кезінде жылудың бөлінуімен (бұл адсорбент пен адсорбтивтің тығыз әрекеттесуін көрсетеді). 3. Активтендіру энергиясының аздығымен (яғни энергетикалық тосқауылдың аласалығы), ендеше адсорбцияның жылдамдығының көптігімен (яғни dГ/dТ және d
2.2 Адсорбция үдерістерін жіктеу. Қаралған жүйелер күрделі болғандықтан адсорбция үдерісінің заңдылықтарын анықтау үшін оларды әр түрлі көрсеткіштер бойынша жіктелулерін қарастырайық; 1. Адсорбент пен адсорбтив арасындағы байланыстардың түріне карай физикалық және химиялық адсорбция болып бөлінеді. Біріншісінде физикалық күштер нәтижесінде фазааралық бетте адсорбциялық қабат түзілсе, екінші жағдайда адсорбциялық үдеріс адсорбенттің функцияналдық арасындағы химиялық реакцияның нәтижесінде болады,яғни олар химиялық күштердің әсерінен байланысады. Бірінші жағдайда адсорбент пен адсорбтивтің арасында молекулааралық, басқаша вандерваалстік күштер болады.Физикалық адсорбция әрқашанда қайтымды. Химиялық адсорбция кезінде адсорбент пен адсорбтив арасындағы байланыс химиялық болады. Хемосорбция көбінде қайтымсыз болады. Мысалы О2-нің С-дегі, СО2-нің СаО-дағы, NH3-тің CuSO4-тегі адсорбциялары. 2. Адсорбция үдерістері адсорбент бетіндегі адсорбтивтің қабатына байланысты мономолекулалық және полимолекулалық болып жіктеледі. Біріншісінде адсорбент бетінде адсорбтивтің моно қабаты болады, ал соңғы жағдайда адсорбент бетінде адсорбтивтің көлемдік қабаты поли қабат болады. 3. Адсорбтив молекулаларының адсорбент бетінің барлық жерінде, ия тек кейбір жерлерінде ғана адсорбциялануына байланысты локализияцияланған және локализацияланбаған болып бөлінеді. Алғашқы жағдайда адсорбент бетінде белгілі бір локализацияланатын адсорбцияда адсорбент бетінің бәрі бірігіп (жұмыс істейді), онда ерекше адсорбцияланатын орталықтар болмайды. 4. Адсорбциялық үдерістер қайтымды және қайтымсыз болып бөлінеді. Адсорбент үдерісі кезінде оған қарама-қарсы үдеріс- десорбция жүретін жағдайлар болады. Бұл кезде адсорбция қайтымды болады. Егер адсорбцияның константасын Ка,ал десорбциясының константасы Кg деп белгілесек ,онда қайтымды адсорбция болу үшін мынадай шарт Kg/Kaǂ0 орындалуы керек.Егер Кg=0 болса, онда адсорбция қайтымсыз болады. 5. Адсорбция кезінде тура және кері үдерістерінің арасында тепе-теңдік болу - болмауына байланысты адсорбцияны тепе-теңдік және тепе-теңдіксіз болса,яғни Kg/Ka=const болса,онда адсорбент қайтымсыз болады. 6. Адсорбциялық құбылыстарды өзара жанасатын фазалардың агрегаттық күйіне байланысты топтаған да жөн. Осыған байланысты бес түрлі адсорбциялық жүйелерді көрсетуге болады. 1. Г/Е - газ бен ерітінді арасындағы адсорбция. 2. С/Е - сұйықтық пен ерітінді арасындағы адсорбция. Мұның бірінші адсорбциядан айырмашылығы ерітіндіден еріген заттың концентрациясының өзгеруі ерітінді мен оның буының арасында емес, басқа сұйықтың арасында болады. 3. С1/С2 - өзара ерімейтін екі сұйықтықтың арасындағы адсорбция. 4. Г/Қ - қатты дене (адсорбент) бетіндегі газдың адсорбциясы. 5. Е/Қ - қатты дене бетіндегі ерітіндідегі еріген заттың адсорбциясы. Капиллярлық конденсация деп аталатын сорбциялық құбылыстың тағы бір түрін айтып кеткен жөн. Бұл құбылыс кезінде адсорбент адсорбтивті (газдар мен буларды) жұтып қана қоймай, оның үстіне өздерінің капиллярларында (түтікшелерінде) конденсациялайды. Газдардың жұтылуына қарап оларды адсорбция құбылысы деуге болар еді. Ал капиллярлардың ішінде конденсацияланған сұйықтың жиналып, олардың барлық көлемде бірдей болмайтындықтан оларды адсорбциялық құбылысына жатқызуға да болады. Алтыншы жіктеудің алғашқы үшеуінде адсорбентіміз сұйықтық болса, төртінші және бесіншісінде – адсорбентіміз қатты дене. Сондықтан олардың өзара айырмашылықтары да бар. Мысалы үшін алғашқы үшеуінде адсорбция шамасын Г беттік керілумен σ байланыстыруға болады. Бізге беттік керілу ұғымы белгілі болғандықтан адсорбция құбылыстарымен толығырақ танысу үшін сол ерітіндімен газ, иә сұйықтық арасында болатын адсорбциялық құбылыстарға тоқталайық.
2.2. Ерітінді мен газ және сұйықтық арасындағы адсорбция. Бетті-активтік заттар (БАЗ) Жеке сұйықтық үшін біз беттік керілуді қарастырған болатынбыз. Онда сұйықтықтың көлемі мен бетінің құрамы бірдей болғандықтан белгілі бір температура мен бөліну беті үшін (мысалы сұйықтықтың буымен) беттік керілуі - тұрақты және қарастырып отырған сұйықтықты сипаттайтын шама. Ерітінділер үшін беттік керілу еріткіштің табиғаты, температура, екінші жанасатын фазаның табиғатына және еріген заттың табиғаты мен мөлшеріне, яғни ерітіндінің концентрациясына тәуелді болатын күрделі шама. Ерітіндінің беттік керілуіне бөлу беттерінде болатын адсорбция құбылыстары да күшті әсерін тигізеді. Беттік еркін энергия F бет (S) пен беттік керілудің (σ) көбейтіндісіне тең: F=S·σ Сондықтан беттік еркін энергия иә беттің кішіреюінің нәтижесінде, иә беттік керілуінің азаюының нәтижесінде ғана азаюы мүмкін. Ерітінділер және коллоидтық химияның т.б. көптеген құбылыстары үшін F кемуінің екінші жолының маңызы зор. Мысал үшін көптеген заттар еру арқылы еріткіштің беттік керілуін азайтады. Ерітіндідегі еритін заттарды сұйықтық пен ауа арасындағы бетте адсорбциялану қабілетіне байланысты екіге бөлуге болады: а) бетті-активтік заттар (БАЗ). ә) бетті-активтік емес заттар (БАЕЗ). Бетті-активтік заттар бетте жиналатын болғандықтан, оң адсорбция болады, яғни Г>0. Бұлай болу үшін бетті-активтік заттардың беттік керілуі еріткіштің беттік керілуінен кіші болу керек: σ<σ0 (бұлай болмаған жағдайда БАЗ бетте жиналуы термодинамикалық қолайсыз) және олар еріткіште аздап қана еру керек. Егер БАЗ еріткіште жақсы ерісе ол беттен еріткіштің көлеміне еніп кеткен болар еді. Сонымен БАЗ бен еріткіштің молекулаларының арасындағы әрекеттесу әрқашанда еріткіштің арасындағы әрекеттесуден әлсіздеу болады. Сондықтан БАЗ көлемнен бетке қарай итеріліп, бетте жиналады. Осының нәтижесінде Г>0. Осы себепті бетте молекула аралық әрекеттесу болғандықтан беттің беттік керілуі кемиді. Су үшін көптеген органикалық қосылыстар БАЗ бола алады. Мысалы органикалық үлкен радикалдары бар қышқылдар, олардың тұздары (сабындар), сульфоқышқылдар және олардың тұздары, спирттер, аминдер т.б. Көптеген БАЗ-дың өздеріне тән ерекшеліктерінің бірі - олардың дифильдік болып келуі, яғни олардың молекулаларының екі бөліктен тұруы. Полярлық топ және полярлық емес көмірсутек радикалдарынан тұрады. Бұдан былай БАЗ-дың дифильдік молекулаларын былайша көрсетеміз:
немесе Мұндағы нүкте (дөңгелек) полярлық (топты, топшаны), ал сызықша полярлық емес радикалды көрсетеді. Бетті-активтік емес заттар (БАЕЗ) (кейде оларды беттік инактивті заттар дейді). Олар беттен көлемге қарай ұмтылатын болғандықтан теріс адсорбцияны байқауға болады, яғни Г<0. БАЕЗ-дың беттік керілуі көбінде таза еріткіштердің беттік керілуінен көп шама, оның үстіне олар жақсы еритін болғандықтан олар көлемге тарайды. Басқаша айтқанда БАЕЗ-дың молекулаларымен еріткіштің молекулаларының арасындағы әрекеттесу еріткіштің молекулаларының арасындағы әрекеттесуден әрқашанда жоғары, міне осының нәтижесінде олар ерітіндінің көлеміне тарайды. Су үшін БАЕЗ - көбінде бейорганикалық электролиттер - қышқылдар, сілтілер, тұздар. Бұлардың молекулаларында гидрофобтық бөліктері жоқ, суда жақсы еріп онымен гидратталатын иондар береді. Органикалық заттардан су үшін БАЕЗ-ға иондалатын және молекулаларының полярлы емес бөлігі жоқ болатын, иә өте аз болатын заттар жатады. Бұндай заттарға мысалы үшін құмырсқа қышқылы және аминдік сірке қышқылы сияқты заттар жатады. Кейбір заттар еріткіште ерігенде оның беттік керілуін өзгертпейді, олар бет пен көлемде бірдей тарайды, яғни Г=0. Әрине мұндай заттардың беттік керілуі еріткіштің беттік керілуімен бірдей не оған жуық шама болады. Беттік керілуді өзгертпейтін заттарды беттік индиференттік заттар (БИЗ) деп атайды. Мысалы су үшін - сахароза, қанттың судағы ерітіндісі судың беттік керілуін өзгертпейді. Алайда қант су мен ауаның арасындағы беттік керілуді өзгертпегенмен, су мен қатты дене немесе басқа сұйықтықтың арасында олардың беттік керілуін өзгертетінін айта кеткен жөн. Әрине соңғы жағдайлар үшін қант БАЗ болып есептелінеді. Ерітіндідегі беттік керілудің еріген заттың табиғаты мен концентрациясына тәуелділігін 2.1 - суреттен көруге болады. Бұндағы 1-қисық БАЗ-дың изотермасы, 2-қисық БАЕЗ-дың изотермасы, 3-қисық БИЗ-дың изотермасы. 1 қисықтан БАЗ-дың концентрациясы өскен сайын алғашқы кезде беттік керілу өте тез кемісе, кейіннен абциссаға параллель болатынын байқауға болады. Оны былайша түсіндіруге болады. Алғашқы кезде сұйықтық пен ауаның бөлу бетінде БАЗ болмағандықтан БАЗ-дың молекулалары бетке кетеді де беттің беттік керілуін кемітеді. Белгілі бір концентрацияда БАЗ молекулалары бетті толық жабады да олардың әрі қарай адсорбциялануына кедергі жасайды. Соның нәтижесінде абциссаға параллель учаскені байқауға болады, яғни бұл беттік керілудің концентрацияға өте аз байланыста болатын жағдайы. Ал аралық жағдайға беттік керілудің кемуінде аралық мәні сәйкес келеді. Ал 2-қисықтан беттік керілудің БАЕЗ-дың концентрациясының өсуіне байланысты аздап көбейетіндігін байқауға болады. БАЕЗ-дың беттік керілуі ерігіштік беттік керілуінен көп болғандықтан және олардың еріткіште жақсы еритіндігінен олар көлемге кетеді. Міне осы себепті беттік керілудің аздап өсетіндігін байқаймыз.
c→ 2.1-сурет. Ерітіндінің беттік керілуінің σ еріген заттың табиғаты мен концентрациясына тәуелділігі.
3-қисықтан заттың концентрациясы өскен сайын беттік керілудің өзгермейтінін байқауға болады, яғни қисық абциссаға параллель, өйткені еріген заттың беттік керілуі еріткіштің беттік керілуі мен бірдей (иә шамалас). Заттардың бетті-активтік болуы олардың табиғатына ғана емес, сонымен қатар (ортаның) еріткіштің табиғатына да байланысты болады. Мысалы суда көптеген заттар беттік активтік қасиет көрсетеді. Өйткені судың беттік керілуі көпшілік сұйықтықтардың беттік керілуінен көп шама (73 эрг/см2). Ал спирттерді алып қарасақ олардың беттік керілуі судың беттік керілуінен аз (22 эрг/см2). Сол себепті суда бетті- активтік қасиет көрсететін заттар спиртте бетті-активтік емес болады. Ерітіндідегі беттік керілудің температураға тәуелділігі. Таза сұйықтың беттік керілуі температура өскен сайын бір қалыпты түзу сызықты кемитіндігін жоғарыда айтқан болатынбыз. Ал ерітінділердің беттік керілуін қарастыратын болсақ, кейбір ерітінділерде температура өскен сайын олардың беттік керілуі түзу сызықты түрде емес максимум арқылы өтетін қисық түрде кемитіні байқалған. Бұл жөнінде көп мәліметтерді П.А.Ребиндердің жұмыстарынан табуға болады. 2.2 суретте таза сұйық (1) пен БАЗ еріген ерітіндінің (2) беттік керілулерінің температураға байланыстылығы сұлбалық түрде көрсетілген. Мұнда 2-қисықтағы максимумның болуы беттік активті заттардың десорбцияның нәтижесінде болады.
Т 2.2-сурет. Беттік керілудің температураға тәуелділігі.
БАЗ десорбцияланған кезде беттік керілу көбейеді де қисықты максимум пайда болады. Ал температура одан әрі өскенде яғни десорбция біткен соң беттік керілу қайтадан кеми бастайды. Әрине еріген заттың беттік активтілігі неғұрлым көп болса, соғұрлым максимум жоғары бролатынын айта кеткен жөн. 2.3. Гиббс теңдеуі Сұйықтық пен газ арасындағы адсорбция құбылысын түсіндіру үшін беттік қабаттағы адсорбцияланған заттың шамасын (Г), ерітіндідегі БАЗ концентрациясын (С) және сұйықтық пен газ арасындағы беттік керілудің (σ) арасындағы байланысты білген жөн. Бұл байланыстылықты (заңдылықты) сұйытылған ерітінділер үшін 1873-75 ж қорытып шығарылған Гиббстің теңдеуімен көрсетуге болады.
Гиббстің бұл теңдеуін әртүрлі жолмен қорытуға болады. Солардың ішінде қарапайымы - Во. Освальдтың қорытқаны. Енді осыған тоқталайық. Беті S см2 тең, беттік қабатында 1 моль еріген заты бар ерітінді болсын, ендеше Егер көлемнен ерітіндідегі еріген заттың өте аз мөлшері бетке шығатын болса, онда беттік керілу dσ-ға азаяды да, соған сәйкес беттік еркін энергия да азаяды.
Беттік энергияның бұл өзгеруі тепе-теңдік жағдайда сол еріген затты ерітіндіден шығаратын осмостың жұмысына тең болады. dA=-Vdπ V - 1 моль зат ерігендегі ерітіндінің көлемі; dπ - ерітіндінің осмостық қысымының өзгеруі; dA=dF олардың мәнін қойып теңестірсек:
Сұйылтылған ерітінділер үшін Вант-Гофф заңын қолдансақ:
V= 1000M /c
с-еріген заттың салмақтық концентрациясына байланысты, М - молекулалық салмақ, π -атм. болса, R=8,3*10-7см3 *атм/град V мен dπ мәндерін орындарына қойсақ,
Бұдан бұл теңдеуді математикалық түрлендіру арқылы Г-ні тапсақ, Гиббс теңдеуін алуға болады:
Әрине бұл теңдеуді сұйылтылған ерітінділер үшін қорытып шығардық, сол себепті бұл сұйылтылған ерітінділер үшін қолданылады. Егер концентрациясы жоғары ерітінділер болатын болса, онда Гиббс теңдеуіндегі С орнына заттың активтілігін ( Гиббс теңдеуін термодинамиканың бірінші және екінші заңдарының біріккен теңдеуінен де қорытуға болады. Ол теңдеу былайша жазылады: dU = TdSs + σds + бұл дифференциалдық теңдеу экстенсивті шамаларға қатысты бір текті және бірінші дәрежелі. Эйлер теоремасы бойынша, мұндай теңдеуді коэффиценттердің тұрақты мәндерінде интегралдауға болады. Физикалық мәні: σ, Т, және μ тұрақты мәндерінде (яғни беттік қабат құрамы өзгермейді. S шамасы шектеулі артады:
Жүйенің барлық ықтимал өзгерістерін қарасытырып, яғни дифференциалдап келесі теңдеуге келеміз:
(3)- теңдеуді кемітіп,
теңдеуін аламыз. Алынған (4) теңдеудің екі жағын да s шамасына бөліп, және тек изотермиялық процестерді (T=const) қарастыратын болсақ, Гиббс теңдеуінің жалпы түріне келеміз:
бинарлы жүйе үшін:
Мұндағы 1 индексі - еріткішке, 2 индексі – еріген затқа сәйкес. Бұл теңдеу Г мен σ арасындағы байланысты береді, бірақ шешімі айқын емес, себебі екі белгісіз шама кіреді. Г1 және Г2. Сондықтан Гиббс келесі шартты қабылдайды: бөліну бетін Г1=0 болған жағдайда дейін өткізуге болады. Онда жоғарыдағы теңдеулерге сәйкес Гиббс теңдеуі:
түріне келеді. Г2 шамасының физикалық мәні: екінші компонеттің (еріген заттың) көлемдік фазаға қарағанда беттік беттік қабат көлеміндегі артық мөлшері.
өрнегін ескере отырып, келесі теңдеулерді алуға болады:
және
(10) өрнек Гиббс теңдеуінің дифференциалдық түрін көрсетеді. Сұйытылған ерітінділер үшін бұл өрнек келесі түрде жазылады:
Гиббс теңдеуі тәжірибе жүзінде Г анықтау арқылы бір емес бірнеше рет тексеріліп оның дұрыс екені көрсетілді. (Мак-Бен, Фрумкиннің тәжірибелері). Гиббс теңдеуіндегі dσ/dc қатынасын Ребиндердің ұсынысы бойынша - беттік активтілік деп атайды және де Гиббстің құрметіне (G)Гиббс деп те атайды. Оның бірлік өлшемі Дж/м2·моль немесе эрг/см2 ·моль. Гиббс теңдеуінен мыналарды байқауға болады: 1.Егер dσ/dc<0 болса, онда Г>0. Бұл еріген затымыз БАЗ болатын жағдайларда болады, яғни беттік керілу БАЗ әсерінен кемиді де, оң адсорбцияны байқауға болады. 2. Егер dσ/dc>0 болса, онда Г<0. Бұл еріген затымыз БАЕЗ болатын жағдайлар. Шындығында да егер БАЕЗ ерісе беттің керілуі көбейеді де, теріс адсорбция болады. 3.Егер dσ/dc=0 болса, онда Г=0. Бұл индиференттік заттарда байқалады, өйткені олар ерігенде беттік керілу өзгермейді, сол себепті адсорбция құбылысы болмайды. Гиббс теңдеуін пайдалана отырып, БАЗ беттік керілуінің изотермасы бойынша, олардың адсорбциясының изотермасын сызуға болады. (2.3-суретті қара). Ол үшін беттік керілу изотермасындағы кез келген бір нүктені алып, суретте көрсетілгендей етіп сол нүктеге жанама және координаталық осьтеріне параллель жүргіземіз. Сонда ордината осіндегі жанама мен нүктеден абциссаға паралелль жүргізілген түзу сызық арасындағы кесіндінің (сол нүктеден ордината осіне жүргізілген параллельдің абциссаға қилысқан кесіндісіне С қатынасы мынаған тең:
2.3-сурет. Беттік керілу изотермасы бойынша адсорбция изотермасын салу.
dσ/dc - мәнін Гиббс теңдеуіне қойып, адсорбция шамасын табамыз:
Міне осылай беттік керілу изотермасындағы бірнеше нүктелер үшін Г-нің сәйкес мәндерін тауып, адсорбция изотермасын сызуға болады. Беттік-активтік заттар үшін Г≈А деп алуға болады. Ленгмюр теңдеуінен шекті адсорбция Г∞ және К константаның мәндерін табады. Ол үшін Ленгмюр теңдеуін түзу сызыққа айналдыратын графиктік тәсілді қолданады: c/Г=Кс+1/КГ∞=с/ Г∞+1/КГ∞ (18) 1/Г∞= α=const
c/Г = ас + b (20 ) Г∞ табу үшін абцисс осіне концентрацияның (с) мәндерін, ал ордината осіне с/Г шамалар қойып, нүктелерді түзу сызықпен біріктіреді. Сурет салу керек.............
α бұрышының котангенсі Г∞ мәнін, ал ордината өсіндегі кесінді s= мұндағы |
|
 десорбция
десорбция /dТ-нің шамаларының өте көптігімен).
/dТ-нің шамаларының өте көптігімен).
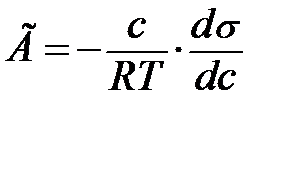
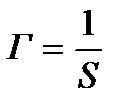
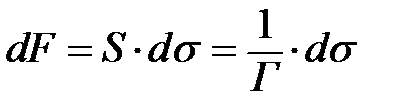
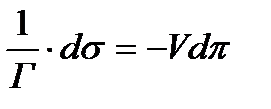
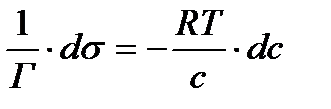
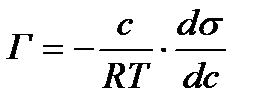
 ) қоюға болады.
) қоюға болады. id
id  (1)
(1) (2)
(2)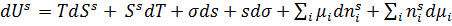 (3)
(3) (4)
(4) (5)
(5) (6)
(6)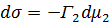 (7)
(7)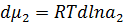 (8)
(8)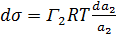 (9)
(9) (10)
(10)
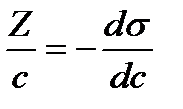

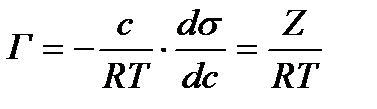
 1/КГ∞= b=const (19)
1/КГ∞= b=const (19)
 -Авогадро саны.
-Авогадро саны.