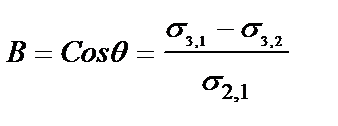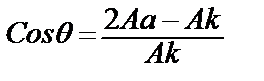|
|
Электролитпен коагуляциялау кинетикасы 2 главаσАВ = σА- σВ Мұндағы: σАВ – екі А жене В сұйықтықтардың арасындағы беттік керілу. σА – А сұйықтығы мен ауының аралығындағы беттік керілу. σВ – В сұйықтығы мен ауаның аралығындағы беттік керілу.
Екі сұйық фазаның арасындағы беттік керілу /И.И Жуков мәліметі/
Бұл кестеден Г.Н. Антонов теңдеуінің ақиқатты өте дәл көрсеткенін білеміз. Мұндағы: А-су, В-органикалық сұйықтық. Температура өскен сайын σ азаяды, өйткені екі сұйықтықтың өзара еруі күшейеді. Екі сұйық өзара толық еритін температурада /дағдарыстық температурасы/ σАВ мәні 0-ге тең болады, σАВ мен температура өзара түзу сызықты байланыста болады. Сұйықтық пен сұйықтық өзара шамалы ерігендегі дисперстік жүйелерге майғындар жатады. Олардың алынуы мен қасиеттері жөнінде арнайы тарауда тағы да тоқталамыз. Сұйықтық пен сұйықтық арасындағы беттік керілуді анықтау үшін де сол сұйықтық пен газ арасындағы беттік керілуді анықтау әдістері сияқты әдістер қолданылады
1.3. Беттік керілуді анықтау әдістері
Қазіргі кезде беттік керілуді анықтаудың 10-шақтыдан астам әдістері бар. Оның бәрі сұйықтық пен газ және сұйықтық пен сұйықтық сияқты екі фазалық жүйелер үшін ғана қолданылады. Оның себебі сұйықтықтардың жылдам қозғалатын молекулаларының әсерінен бөлу беттерінің өзгеруін қайтымды етіп және оңай іске асыруға болады. Ал қатты заттардың беттік керілуін тікелей өлшеу қиын, сондықтан көбінде оларды жанама жолдармен анықтайды. Беттік керілуді анықтау тәсілдерін үш топқа бөлуге болады. 1. Статикалық әдістер: · Капилярдағы сұйықтықтың көтерілу әдісі; · Жатқан не ілінген тамшы (көпіршік) әдісі; · Сұйық беттік қабаттың қисықтық радиусын өлшеу әдісі; · Сақинаны немесе табақшаны теңестіру әдісі (Вильгелми әдісі). 2. Жартылай статикалық әдістер: · Көпіршік не тамшы түзілуінің максималдық қысым әдісі; · Сақинаны беттен үзу әдісі; · Тамшыларды санау не өлшеу әдісі; 3. Динамикалық әдістер: · Капилярлы толқындар әдісі; · Тербелмелі ағыстар не тамшылар әдісі; Коллоидтық химиялық жалпы практикумдарында көбіне қолданылатын әдістерге жартылай статикалық көпіршік түзілуінің максималды қысым әдісі (Ребиндер әдісі) және тамшыларды санау әдісі (сталогмометрлік) жатады. Осы көптеген тәсілдердің ішінде ең көп тараған 4 әдіске қысқаша тоқталайық:
1.3.1 Капиллярлық көтерілу әдісі
Бұл өте дәл, бірақ капиллярларға жұғатын сұйықтар үшін қолданылатын, төменгі теңдеуге негізделген әдіс:
r - Капиллярдың радиусы. h - Капиллярдағы сұйықтықтың көтерілуі биіктігі. d - Сұйықтықтың тығыздығы /ұшқыш сұйықтықтар үшін d-d1 қолданылады, мұндағы d1 - сұйықтықтың буының тығыздығы/ g – еркін түсу үдеуі.
1.3.2 Сақинаны, иә пластинканы үзу (айыру) әдісі
Бұл жалпы физика курсынан белгілі, төменгі қарапайым теңдеуге негізделген әдіс:
L – сақинаның, иә пластинканың периметрі Бұл әдіс де жұғатын сұйықтарға қолданылады. Бірақ бұл әдіс беттік керілу шамасын өте дәл көрсете алмайды.
1.3.3. Тамшыларды санау, иә сталагмометрлік әдіс
Бұл әдіс те өте дәл емес, солай бола тұра өте қарапайым болғандықтан зертханалық жұмыстарда кең таралған әдіс. Бұл тәсіл Траубе сталогмометрі деп аталатын капиллярлық тесігі бар құралдан белгілі-бір V - көлем сұйық шыққан кезде тамшыларды тікелей санауға негізделген. Мұнда екі түрлі сұйықтықтың беттік керілулерінің қатынасы олардың бірдей радиусты тесіктен тамған тамшыларының салмақтарының қатынастарына тең, өйткені Р=2 π∙r∙ σ
Мұндағы n-V көлемдегі тамшының санын еске ала отырып мынаны жазуға болады:
Бұдан Егер екінші сұйығымыз стандарттық, ал біріншісі зерттелетін сұйықтық болса, онда бұл теңдеуді былай жазуға болады:
Мұндағы σ0, d0, n0 - деп отырғанымыз стандарттық /белгілі бір/ сұйықтықтың, көбінде судың, беттік керілуі, тығыздығы және тамшылар саны, ал Мұнда d0, do, σ0 - олардың мәнін даяр күйде кестеден алатын болғандықтан, қарастырып отырған тәсіліміз су мен іздестіріп отрырған сұйықтықтың тамшыларын есептеумен ғана шектеледі.
1.3.4. Көпіршіктердің ең үлкен қысымына негізделген әдіс
Бұл-қазіргі кездегі ең ыңғайлы, әрі универсалды және де беттік керілуді аса күшті дәлдікпен (әсіресе Ребиндер құралымен істелгенде) анықтайтын тәсіл. Сондықтан бұл әдісті кейде Ребиндер әдісі деп те атайды. Бұл суға батырылған капиллярдағы ауаның көпіршігін үзу үшін қажет ең үлкен қысымның беттік керілуге пропорционал болатынына негізделген.
Егер бірінші сұйықтық зерттелетін, ал екінші сұйықтық стандарттық болса, онда: Мұндағы: х – зерттелетін, ал 0 – стандарттық сұйықтыққа тән шамалардың индекстері. Мұндағы: Р1, Р2 - деп отырғанымыз, ұшының радиусы – r капиллярдағы іздеп отырған және стандарттық сүйықтардағы көпіршіктердің түзілетін, қысылып және үзілетін қысымдардың ең үлкен шамасы: h1, h2 – деп отырғанымыз көпіршік үзілген кездегі Р1 және Р2 сәйкес келетін монометрлік түтікшедегі сұйықтықтардың биіктіктері. Бұл әдіс жоғарыда айтылған әдістерді қолдана алмайтын жағдайда, екі сұйықтық арасындағы беттік керілуді анықтау үшін өте қолайлы. Әрине бұл жағдайда беттік керілуді анықтау ауа болмағандықтан көпіршіктің үзілуі емес, екі сұйықтықтың кез келетін тамшысының тамуына негізделеді. Біз бұл жерде тек әрбір әдістің негізімен таныстық, ал олармен зертханалық жұмыс жасаған кезде, коллоидтық химияның практикалық нұсқауларын оқып толығырақ танысуға болады.
1.4. Жұғу құбылысы. Лиофильдік және лиофобтық беттер
Қатты дененің беттік керілуін, оларды жаңа беттердің пайда болатын қайтымды үдерістер болмағандықтан тікелей өлшеу қиынға соғатынын айттық. Сондықтан қатты дененің беттік керілуін жанама эксперименттік жолмен, иә Борн мен Френкель жасаған кристалдық тордың электростатикалық теориясына сүйене отырып теориялық жолмен есептеуге болады. Әрине қатты дененің табиғатына байланысты олардың беттік керілуі әртүрлі, бірақ әрқашанда сұйықтықтардың беттік керілуінен әлдеқайда көп шама болады. Олардың шамасы жүздеген және мыңдаған эрг/см2. Кейбір жұғу және адсорбция сияқты құбылыстарда қатты денелердің беттік керілуі азаятынын байқауға болады. Сұйықтықтар мен қатты денелер бетіндегі болатын жұғу құбылысына тоқталайық.
1.4.1 Жұғу құбылысы Сұйықтық тамшысы қатты дененің бетіне түскенде мындай үш түрлі жағдай болуы мүмкін: 1. Тамшы қатты дененің бетіне жайылып кетеді. 2. Тамшы қатты дене бетінде шар тәрізді болып қалуы мүмкін. 3. Тамшы қатты дененің бетінде, онымен шеттік бұрыш жасай аздап жайылады. Шеттік бұрыш деп үш фазаның қиылысқан нүктесі арқылы сұйықтық тамшысына жүргізілген жанаманың сұйықтық жағынан алынған бұрышты айтады. /1.4. суретте стрелкамен көрсетілген/
1.4. - сурет. Жұғудың шеттік бұрыштары
Егер сұйықтық тамшысы қатты дене бетіне толық жайылып кетсе, иә сүйір бұрыш жасай жайылса, онда ол бетке сұйықтық жұғады деп қарастыруға болады. /1.4а сурет/ Әрине қатты дене бетіне, олардың ауа аралығында беттік керілуін азайтатын сұйықтықтар ғана жұғады. Мысалы үшін су полярлы минералдық заттардың /яғни иондық, иә полярлығы байланысы бар заттардың/ бетіне жұғады, яғни онда денелердің бетінде су иә толық жайылып кетеді де, иә сүйір бұрыш жасай жайылады. Қатты дененің су жұғатын беттерін - гидрофильдік беттер / су ұнататын бет/, ал су жұқпаса, онда - гидрофобтық беттер /суды ұнатпайтын/ деп айтады. Ендеше су жұқпайтын беттерде су тамшысы жайылмайды және доғал бұрыш жасай орнығады. Су орнына басқа сұйықтықтарды қарастырғанда олардың жұғу жұқпауына байланысты беттер жалпы алғанда лиофильдік және лиофобтық беттер боп екіге бөлінеді. Лиофильдік бет деп сұйықтық жұғатын, ал лифобтық деп сұйықтық жұқпайтын бетті айтады. Сонымен сұйықтық жұққан кезде шеттік бұрыш сүйір, яғни Ө < 900, ал жұқпаған кезде Ө > 900. Ал сұйықтық қатты дене бетінде толық жұққанда, онда Ө=0 тең, ал толық жұқпағанда шеттік бұрыш 1800-ке тең болмайды, өйткені аз да болса тамшының ауырлық күші әсер етеді. 1.5. – сурет. Жұғуды беттік керілу күштері арқылы сипаттау
Қатты дене бетінде сұйықтықтың тамшысына түсірілген, онда толық жұқпаған кездегі жағдайда қарастырайық. /1.5 - сурет/. Бұнда жұғу периметрі деп әрекеттесіп отырған үш ортаның - сүйықтықтың 2, ауаның 1 және қатты дененің 3- шекарасын айтады. Осы жұғу периметріне үш түрлі күш әсер етеді, олар: 1. Сұйықтық пен қатты дене арасындағы беттік керілу – σ3,2 2. Сұйықтық пен ауаның арасындағы беттік керілу – σ2,1 3. Қатты дене мен ауаның арасындағы беттік керілу – σ3,1. Тепе-теңдік шеттік бұрышы осы үш күштің проекцияларының қосындысы 0-ге тең болғанда орындалады. Бұл тепе-теңдік жағдайды (1807 ж.) Юнг формуласы арқылы жазуға болады:
Бұдан Бұл формуланы термодинамикалық жолмен Адамсон да қорытып шығарған болатын. Адамсон бойынша сұйықтық бетте аздап жылжығанда тамшымен жабылған бет ΔS-ке артады. Бұл кезде беттің еркін энергиясының өзгерісі ΔGs мынадай болады:
ΔGs = ΔS(s3,2 - s3,1) + ΔSs2,1 cos(q+Δq) Мұндағы Δθ –шеттік бұрыштың өзгерісі. Тепе-теңдік жағдайда:
s3,2= s3,1 + s2,1 cos q=0; бұдан: cosq = (s3,1 - s3,2)/s2,1. СоsӨ шамасы сұйықтықтық бетке жұғу құбылысын сандық түрде сипаттайтын болғандықтан, оны жұғу деп атап, В деп белгілеу келісілген. Ендеше толық жұғу болғанда /Ө=0/ В= + 1, ал толық жұқпайтын гипотезалық жағдайда /Ө=180/ В= - 1: Сонымен сұйықтық молекулаларының арасындағы әрекеттесу күші сұйықтық молекулалары мен қатты дене молекулаларының әрекеттесу күшінен аз болса жұқпайды. Жұғу құбылысын ауа орнына бірінші сүйықтық ерімейтін және тығыздығы бірінші сұйықтықтың тығыздығынан аз, екінші бір сұйықтық алғанда да байқауға болады. Әрине екі сұйықтықты қарастырғанда қатты дене бетіне қайсысының полярлығы қатты дененің полярлығына жақын болса, сол сұйықтық жұғады. Жақсы жұғатын сұйықтықты қарастырып отырған бет үшін таңдамалы жұғу қабілеті күшті сұйықтық деп айтады. Таңдамалы жұғу құбылысын П.А. Ребиндер зерттеген болатын. Егер қатты дене бетіне таңдамалы түрде су жұғатын болса, шеттік бұрыш сүйір болады да Ө<90, B=CosӨ>0, онда бетті жоғарыда айтылғандай гидрофильдік бет деп айтады. Судың таңдамалы жұғуы су мен беттің полярлығының айырмашылығы, полярсыз көмірсутек пен беттің полярлығының айрмашылығынан аз болғанда байқалады. Су үшін гидрофильдік беттерге мынадай заттардың беттер жатады: кварц, шыны, гипс, малахит, силикаттар, карбонаттар сульфаттар, және металдардың оксидтері және т.б. Органикалық заттардың ішінде гидрофильдік бетке целлюлоза беті жатады. Егер қатты денеге көмірсутек жұғатын болса, су үшін Ө>90, ал Егер Ө=900 болса, аралық жағдай болады да, онда екі сұйықтықта да таңдамалы жұғу болмайды. Біз жоғарыда жұғу құбылысын шеттік бұрыш арқылы сипаттадық. Шеттік бұрышты анықтау үшін тамшы тамғызып оның көлеңкесін сәуле шоғыры арқылы экранға түсіреді де, сол көлеңкедегі үш фазаның қиылысқан нүктесі арқылы тамшыға жанама жүргізіп бұрышты өлшейді. Ал егер өзара араласпайтын /ерімейтін/ сұйықтықтарда шеттік бұрышын жеңіл сұйықтың құйылған ыдысқа пластинканы горизонтальдық түрде батырып, оған екінші сұйықтықтың /ауыр сұйықтықтың/ тамшысын тамызып жоғарыда айтылғандай етіп табады. Әрине бұл-шеттік бұрышты анықтаудың қарапайым тәсілі, ал оны анықтаудың өте дәл, және күрделі тәсілдері коллоидтың химияның практикумдерінде жазылған. Шеттік бұрыштың шын мәнін табу өте қиынға соғады. Өйткені қатты дененің бетінде әрқашанда бетті ластайтын басқа заттардың аздаған мөлшері әсер етеді. Көптеген металдардың беттері тотығып, тотықтардың бөлінбейтін пластинкаларынан тұруы мүмкін. Осы себепті шеттік бұрышты өлшегенде әрі таза, әрі тотықбаған беттермен жұмыс істеу керек. Бұдан басқа қатты денелердің беттері ауаны жақсы адсорбциялайтыны белгілі. Ал адсорбцияланған ауа сұйықтықтың жұғуын нашарлатады, өйткені сұйықтық бетте жайылу үшін, сол беттегі адсорбцияланған ауаны ығыстырып шығаруы керек. Осы себепті тепе-теңдік беттік бұрышы бірден емес белгілі бір уақыттан кейін қалыптасады. Тепе-теңдік беттік бұрыштың осылай кешігіп қалыптасуын жұғудың гистерезисі деп атайды. Осындай гистерезистің әсерінен кейде беттік бұрыш өзінің тепе-теңдік мәніне жетпейді де. Жоғарғы да айтылғандай ауаны ығыстыру арқылы болатын гистерезисті кейде жұғудың кинетикалық гистерезисі деп айтады. Одан басқа бет кедір-бұдыр болғанда кедергі күшін жеңу әсерінен болатын жұғудың статикалық гистерезисі де болады. Сондықтан беттік бұрышты анықтағанда гистерезисті болдырмау үшін беттік бұрышты төмендегідей әдістемемен өлшейді. Қатты денені жұғатын сұйықтық құйылған ыдысқа батырады. Сұйықтық толық жұққан кезде оның бетіне астындағы шыққан ауа көпіршігін тұмсығы қайырылған тамшуыр арқылы орнықтырады да, оның беттік бұрышын жоғарғы да айтылғандай өлшейді. Тек өлшегенде ауа жағынан емес сұйықтық жағынан есептеу керек. Бұл жолмен біз жұғудың кинетикалық гистерезисін болдырмаймыз, ал жұғудың статикалық гистерезисін болдырмас үшін дененің беті таза және тегіс болуы керек. Жұғу құбылысын шеттік бұрыштан басқа адгезия жұмысы, жұғу жылуы сияқты шамалар арқылы сипаттауға болады. Әсіресе бұл шеттік бұрышты өлшеу қиынға соғатын жағдайларда өте қолайлы. Енді осы шамаларға тоқталайық.
1.4.2. Адгезия және когезия жұмыстары
Бізге фазаның ішіндегі молекулалардың арасындағы күштің когезиялық күш, ал әртүрлі фазаның молекулалаларының арасындағы күштің адгезиялық күш екені белгілі. Енді адгезия және когезия жұмыстарын қарастырайық. 1.6-суретте көрсетілгендей бірі тек су, ал екіншісіне су және май құйылған, екі цилиндрді қарастырайық. Жеңілірек болу үшін, цилиндрдің көлденең қимасының ауданы 1 см2 етіп алайық. Су құйылған цилиндрді, екіге бөлсек, онда су мен ауаның бөлу беті 2 см2 болады. Ендеше біз сол су молекулаларының арасындағы /байланысу/ тіркелу күштерін жеңіп, белгілі бір жұмыс істедік. Бұл жұмысты когезиялық жұмыс дейді. Сонымен когезиялық жұмыс деп бірдей сұйықтықтардың фазаларының арасындағы күшті жеңуге кететін және әрқайсысы 1 см2 сұйықтық пен ауа /газ/ арасындағы болатын екі жаңа бет беретін жұмысты айтамыз. Ендеше су үшін когезиялық жұмыс мынаған тең: Ак = 2σС: мұндағы σС – судың беттік керілуі. Ал май үшін: Ак = 2 σМ: мұндағы σМ – майдың беттік керілуі.
1.6. – сурет. Енді су мен май құйылған цилиндрді екіге бөлу үшін және жаңа бет түзу үшін су молекуласы мен май молекулаларының арасындағы адгезиялық күшті жеңу керек. Ол күшті жеңе отырып біз адгезиялық жұмыс жасаймыз. Сонымен адгезиялық жұмыс деп екі сұйықтық молекулаларының арасындағы күшті жеңе отырып сол екі сұйықтықтың әрқайсысының ауамен 1 см2 бет түзуге кететін жұмысты айтады. Аа = σА + σВ – σАВ: Бұл теңдеуді бірінші рет Дюпре көрсеткендіктен Дюпре теңдеуі деп атайды. Адгезия мен когезияның көптеген технологиялық операцияларда және биологиялық үдерістерде маңызы зор. Мысалы, екі денені желімдеу үшін, желімнің адгезиялық жұмысының мәні өте үлкен шама болу керек. Соңғы кездерде жай келеткалармен рак ауруына шалдыққан клеткалардың адгезиялық қабілеттерінің әртүрлі екені анықталды. Адгезия және когезия жұмыстары арқылы жұғу құбылысын сипаттауға болады. Юнг формуласы бойынша мынаны жазуға болады:
Ак=2·σ1.2; ал Aа= σ1.3+ σ1.2- σ2.3 еске ала отырып жұғу құбылысын былайша сипаттауға болады:
Бұдан адгезиялық жұмыс пен когезиялық жұмыстың айырмашылығы неғұрлым көп болса, соғұрлым сұйықтықтың жақсы жұғатыны көрініп тұр. Адгезияның артуымен жұғу жақсы жүреді. Яғни фазааралық әрекеттесу (адгезиялық күштер) тамшыны жаюға, ал когезиялық күштер тамшыны жинап, сфераға айналдыруға тырысады. Адгезиялық және когезиялық жұмыстар арқылы жұғу шарттарын анықтауға болады: Жұғу - Wa>0,5Wc Жұқпау - Wa = 0 Шексіз жайылу - Wa = Wc Wa - Wc айырымын жайылу коэффициенті деп атайды. Wa>Wc Дюпре теңдеуіне қайшы келеді, себебі теңдеу бойынша, Wa<Wc. Бірақ, Дюпре мен Юнг теңдеулері тепе-теңдік шартымен шектеледі, ал жайылу тепе-теңдіксіз үдеріс, сондықтан ол үшін жоғарыдағы теңдеулерді қолдануға болмайды. |
|



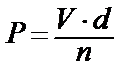
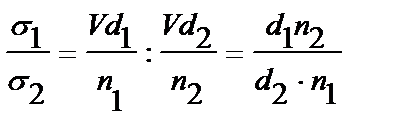
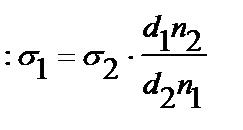
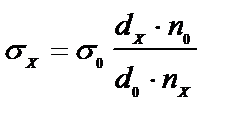
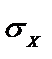 ,
,  ,
,  - зерттелетін сұйықтықтың сәйкесті шамалары.
- зерттелетін сұйықтықтың сәйкесті шамалары.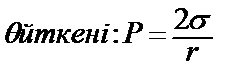

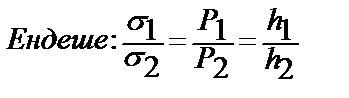
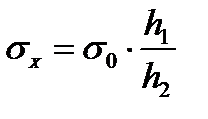

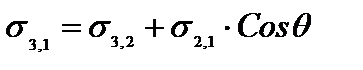
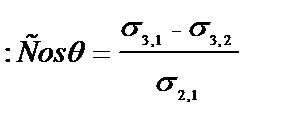
 болады. Ендеше:
болады. Ендеше: