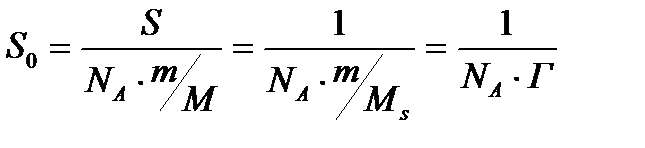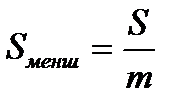|
|
Электролитпен коагуляциялау кинетикасы 5 главаδ=Г∞ мұндағы М – БАЗ-дың молекулалық массасы, ρ-БАЗ-дың тығыздығы.
2.4. Шишковский теңдеуі. Гиббс теңдеуінен Лэнгмюр теңдеуіне ауысу Ерітіндідегі беттік керілудің еріген заттың (БАЗ) концентрацияға тәуілділігі Шишковский теңдеуіне бағынады. (1908 ж). Киевте Шишковский қаныққан органикалық қышқылдардың судағы ерітіндісін зерттей отырып, ерітіндінің беттік керілуінің еріген заттың концентрациясына тәуілділігін тәжірибеден алынған мәліметтерге сүйене отырып, былайша көрсеткен болатын: ∆σ=σ0-σ=σ0·B·ln(C/A+1) мұндағы σ 0-судың беттік керілуі; σ - ерітіндінің (концентрациясы С тең) беттік керілуі; А,В - тұрақты шамалар. В-бетті активтік заттардың табиғатына байланыссыз, ол бөлмелік (200С) температура үшін 0,2 тең тұрақты шама; 1/А - бұл бетті активтік заттардың әрқайсысына әртүрлі болатын тұрақты шама, кейде оны меншікті капиллярлық тұрақтылықдеп атайды. Шишковский теңдеуі көбінде молекулаларында көміртек атомдары 8-ден кем болып келетін органикалық қышқылдардың беттік керілуін есептеуге өте дұрыс мәліметтер береді. 1917 ж Лэнгмюр Шишковскийдің теңдеуінің диференциалдық түрін пайдалана отырып, Гиббстің теңдеуінен Лэнгмюр теңдеуіне ауысуға болатынын көрсетті. Шындығында да Шишковский теңдеуін былайша жазуға болады:
Мұны дифференциалдасақ:
немесе:
Енді Гиббстің теңдеуіндегі
және 1/А- ны К деп белгілесек: Г=ГmaxKC/(l+KC) немесе:
Бұл соңғы теңдеу - Лэнгмюр теңдеуі. Сонымен Шишковский теңдеуіндегі 1/А заттың меншікті капилярлық тұрақтысы Лэнгмюр теңдеуіндегі тұрақты шама К-ға тең. Біз жоғары айтылғандардан Шишковский теңдеуінің термодинамикалық жолмен қорытылған Гиббс теңдеуі мен молекулалық-кинетикалық негізге сүйене отырып қорытылған Лэнгмюр теңдеуіне байланыстыратын аралық теңдеу екенін байқауға болады. Бұл теңдеудегі тұрақты шама 1/А-ның яғни меншікті капилярлық тұрақтының БАЗ құрылыстарына байланыстылығын Дюкло мен Траубе жасаған заңдылыққа сүйене отырып, көрсетуге болады.
2.5. БАЗ-дың құрылысы мен шамаларының газ бен ерітінді арасындағы адсорбцияға әсерлері. Траубе - Дюкло ережесі Біз бұрын БАЗ-дың молекулалары дифильдік болып келетінін айтқан болатынбыз. Онда БАЗ-дың полярлық бөлігі үлкен дифильдік моменті болатын функционалдық топтардан тұратын. Мысалы -СООН; -ОН; -NH2; -SН; -NО2; -NСS; -СНО; - SО3Н, сияқты функционалдық топтар. Ал БАЗ-дың полярлық емес бөлігі алифаттық немесе ароматтық радикалдардан тұратын. Міне осы БАЗ-дың радикалдарының ұзындықтары олардың беттік активтілігіне әсерлерін тигізеді. Алғаш Дюкло (1878 ж), кейінірек Траубе (1891 ж),қаныққан органикалық қышқылдардың судағы ерітінділерінің беттік керілуін зерттей отырып, олардың ерітінді ауа арасындағы активтілігі радикалдардың ұзындығы артқан сайын көбейетіндігін байқады. Олардың радикалдары бір СН2 тобына артқан сайын оған сәйкес беттік активтілігі 3-3,5 (орташа 3,2) есе артатынын да Траубе мен Дюкло көрсеткен. Сол себепті бұл заңдылықты Траубе - Дюкло ережесі деп атайды. Мұны басқаша былайша да тұжырымдауға болады. Егер қаныққан органикалық қышқылдардың радикалдарының ұзындықтары арифметикалық прогрессиямен өссе, оларға сәйкес беттік активтілік геометриялық прогрессиямен өседі. Міне дәл осындай заңдылықты Шишковкий теңдеуіндегі 1/А мәнінен де байқауға болады. Оның шамасы БАЗ-дың молекуласының ұзындығына байланысты жоғарғы заңдылыққа сәйкес өзгереді. Алғаш Дюкло, кейінірек жалпы түрде Траубе көрсеткен бұл заңдылықты былайша түсіндіруге болады. Көмірсутек радикалдарының ұзындығы өскен сайын олардың судағы ерітіндісі азаяды да олар көлемнен бетке қарай ұмтылады. Дюкло-Траубе ережесін адсорбция жұмысы арқылы негіздеуге болады. Оны алғаш Лэнгмюр көрсеткен болатын. Адсорбциялық қабаттың қалыңдығын δ деп белгілейік. Сонда бұл қабаттағы орташа концентрация Г/ δ болады. Термодинамикадан газды V1 көлемнен V 2 көлемге дейін қысқандағы максималдық жұмыс былай жазылатынын білеміз: A=RTln (V1/V2) Концентрациясы с1 және с2 екі идеалды ерітінді үшін π1V1= π2V2 немесе V1/V2=π2/ π 1, ендеше : A=RTln π2/ π1=RTln c2/c1 мұндағы П-осмостық қысым. Еріген затты көлеммен бетке шығаратын жұмыс, яғни адсорбция жұмысы мынаған тең: A=RTln Гомологтық қатардағы екі мүшесінің адсорбциясының максималдық жұмыстарының айырмасы : Аn –An-1=RTln Бұл теңдеуден адсорбция жұмысы көмірсутек тізбегі бір СH2-ге артқанда бірдей санға артатыны көрініп тұр . Ол Траубе-Дюкло ережесі сақталатын аз концентрацияларда тізбектегі барлық СH2 топтары бетке қатысты бірдей жағдайда болғанда ғана , яғни тізбек бетке параллель жатқанда болады. БАЗ молекулаларының бетте бағытталып орналасуына осы тарауда адсорбциялық қабаттың құрылысын қарастырғанда да тоқталамыз. Дюкло - Траубе ережесі тек органикалық қышқылдар емес спирттер, аминдер т.б. гомологтың қатарларына да сақталады екен. Бұл жоғарыда тұжырымдағандай Дюкло - Траубе ережесі тек бөлмелік температурада иә бөлмелік температураға жуық температураларда орындалады. Ал жоғарғы температурада 3,2 қатынасы 1-ге дейін азаяды, оның себебі температура өскен сайын десорбцияның нәтижесінде беттік активтілік кемиді. Гомологтардың беттік активтілігінің айырмашылығы азаяды. Тағы бір айтатын жағдай осы Дюкло - Траубе ережесі БАЗ-дың судағы ерітінділеріне ғана қолданылады. Олардың полярлық емес еріткіштердегі, яғни органикалық еріткіштердегі ерітінділері үшін Дюкло-Траубе ережесі керісінше болады. Өйткені радикалдардың ұзындықтары өскен сайын олардың (БАЗ-дың) органикалық еріткіштердегі ерігіштіктері өседі де, олардың беттен көлемге тарауы артады.
2.6. Ерітінді мен газ арасындағы адсорбциялық қабаттардың құрылысы Ерітінді мен газдың арасындағы адсорбция құбылысын біз бұған дейін термодинамикалық тұрғыдан қарастырдық. Енді ерітінді мен газ арасындағы БАЗ-дың молекулаларының бағыталып орналасуы мен адсорбциялық қабаттардың құрылысына тоқталайық. Бөлу беттеріндегі адсорбциялық қабаттың құрылысы туралы түсінік алу үшін суда ерімейтін әртүрлі сұйықтықтардың судағы тамшыларын қарастырайық. Әрине бұл тамшылар судың бетінде не линза тәрізді тамшы күйінде, не су бетінде жайылып кетуі мүмкін. Бірінші жағдайды сұйықтық молекулаларының арасындағы тартылыс (әрекеттесу) су молекулалары мен сұйықтық молекулаларының арасындағы әрекеттесуден көп болған жағдайда байқауға болады. Ал бұл әрекеттесулердің шамасы керісінше болса, онда сұйықтың су бетінде жайылуын, яғни екінші жағдайды байқауға болады. Тамшының түзілуін қарастырып отырған сұйықтығымыз полярлық емес болғанында байқаймыз. Ал сұйықтықтың молекулалары дифильдік болып келсе, онда олар су бетінде жайылып, беттік мономолекулалық қабаттар түзеді. Су бетінде жайылатын, бірақ суда ерімейтін заттарға жоғарыда айтылған дифильдік БАЗ жатады. Су бетінде мономолекулалық қабыршықтар үш жағдайда болуы мүмкін: газ тәрізді, сұйықтық және қатты жағдайда. Сұйық және қатты беттік қабыршықтарды кейде конденсацияланған қабыршықтар деп те атайды. Мономолекулалық қабаттардың агрегаттық күйі қабыршықтардың молекулаларының арасындағы әрекеттесумен анықталады. Осы қабыршықтардың түрлеріне жеке-жеке тоқталайық.
2.6.1. Газ тәрізді беттік қабыршықтар Қабыршықта молекулалар арасындағы тартылу күші өте аз шама болса, онда БАЗ молекулалары судың бетіне жайылуға тырысып бір-бірінен үлкен қашықтықта болады. Жылулық қозғалыстың нәтижесінде молекулалар су бетінде бір-біріне тәуелсіз қозғалады да,беттік қысым тудырады. Бұл қысым бағыты жағынан беттік керілуге қарама-қарсы бағытталған болады. Бұндай қабыршықтарды (кейде оларды БАЗ-дың қабаттары деп те атайды) екі өлшемдік газ ретінде қарастыруға болады. Өйткені, адсорбциялық қабаттағы молекулалар судан айырылмайтын болғандықтан олар тек екі бағытқа ғана жылжиды. БАЗ-дың, яғни екі өлшемдік газдардың молекулаларының бетке орналасуы 2.4а суретте көрсетілген.
2.4-сурет. БАЗ-дың молекулаларының бетте орналасуы а)-екі өлшемдік газ, б)-конденсацияланған қабыршықтар үшін.
Суда газ тәрізді қабыршықтар беретін заттарға дифильдік молекулалары бар органикалық қосылыстар жатады. Ондағы радикалдардың ұзындығы өте кіші және өте үлкен болмауы керек. Мысалы қаныққан органикалық қышқылдар үшін радикалдағы С атомдарының саны 12-ден кем және 20-22-ден артық болмауы керек. Алифаттық спирттер мен аминдер де молекулалық салмақтары өте үлкен болмаса олар да су бетінде газ тәрізді қабыршықтар береді. Біз үш өлшемдік газдар мен екі өлшемдік газдардың ұқсастығын қарастырайық. Жоғарыда олардың ұқсас қасиеттерінің бірін айтып кеттік. Ол екеулерінің де қысым тудыратындығы, тағы бір ұқсастығы олардың екеуіне де газ күйінің теңдеуін жазуға болады. Оны былайша көрсетуге болады. Егер жүйедегі БАЗ мөлшері өте аз болса, яғни бетте екі өлшемдік газ болған жағдайда мынаны жазуға болады: σ0 – σ=∆=K·C Бұны дифференциалдасақ: -dσ=d∆=K·dc Соңғы теңдіктегі dσ-ның мәнін Гиббс теңдеуіне қойсақ:
1 моль БАЗ-дың екі өлшемдік газ күйіндегі бетін ω деп белгілейік.
Г-ның мәнін қойсақ: Бұл теңдеудің 1 моль газ үшін жазылатын Клапейрон - Менделеев теңдеуіне ұқсас екенін көруге болады: PV=RT Шындығында Клапейрон-Менделеев теңдеуінде V үш өлшемдік газдың көлемі, ал ω екі өлшемдік газдың көлемі, яғни беті. Клапейрон - Менделеев теңдеуіндегі Р-қысым, ал жоғарғы теңдеудегі БАЗ-дың әсерінен беттік керілудің азаюы, басқаша ол екі өлшемдік газдың қысымын көрсететін шама. Үш өлшемдік реалдық газдардың күйінің теңдеуі өзімізге белгілі Ван-дер-Ваальс теңдеуімен жазылады: (Р+а/V2)(V -в) =RT Осыған ұқсас екі өлшемдік газдың жоғарғыдағыға сәйкес, күйінің теңдеуін А.Н.Фрумкин көрсеткендей былайша жазамыз: (Δ+α/ω2)(ω-β) =RT Бұл соңғы теңдеудегі α мен β шамалары, Ван-дер-Ваальс теңдеуіндегі а мен в шамаларына сәйкес мұндағы α/ω2 түзетпесі радикалдардың белгілі бір ұзындықта олардың арасындағы тарту күштерін көрсетеді.
2.6.2. Конденсацияланған (қатты және сұйық) қабыршықтар Біз жоғарыда БАЗ-дың молекулаларының арасында әрекеттесу болмаған жағдайды қарастырдық. Егер БАЗ-дың молекулаларының радикалдарының арасындағы әрекеттесу күшті болса, онда олар бірігіп конденсацияланған қабыршықтар түзеді. Бұлардың газ тәрізді қабыршықтардан айырмашылығы бұларда молекулалардың жылулық қозғалысы өте қиын болады. Бұндай қабыршықтарда БАЗ-дың молекулалары бір-біріне параллелль, бетке перпендикуляр болып орналасады. Су үшін бұндай қабыршықтарды беретін заттарға органикалық дифильді, радикалдары ұзын болатын БАЗ жатады. Өйткені неғұрлым радикалдар ұзын болса, соғұрлым олардың арасында әрекеттесу күшті болады. Конденсацияланған қабыршықтардың кейбір жағдайларда газ тәрізді қабыршыққа айналатынын айта кеткен жөн. Мысалы жоғарғы температурада олар оңай газ тәрізді қабыршықтарға айналады. Конденсацияланған қабыршықтар көбіне сұйық болып, келеді де оларда молекулалардың қозғалуы (жылжуы) оңайырақ. Егер радикалдардың арасындағы әрекеттесу өте жоғары болса, онда қабыршықтағы молекулалардың қозғалуы қиын болғандықтан оларды қатты дене ретінде қарастыруға болады. Бұндай қабыршықтар радикалдарындағы С атомдардың саны 20-24-тен көп болатын дифильдік молекулаларда болады. Қатты және сұйық қабыршықтарды бір-бірінен былайша ажыратуға болады. Қабыршық бетінде жеңіл ұнтақ сеуіп оны жайлап үрлесек, егер пленка қатты болса, ұнтақ жылжымайды да, егер қабыршық сұйық болса ұнтақ сұйықтық бетінде жылжиды. Осы айтылған қабыршықтардың түрінен басқа тағы дасозылған қабыршықтардеп аталатын қабыршықтар болады. Олар қасиеті жағынан газ тәрізді қабыршықтар мен конденсацияланған қабыршықтардың аралығында болады. Оларды конденсацияланған қабыршықтарды жоғарғы температура беру арқылы алуға болады. Белгілі бір температура аралығында конденсацияланған қабыршықтар созылады да, температураны әрі үлкейту оларға әсерін тигізбейді, яғни пленканың ауданы өзгермейді. Созылған қабыршықтарда радикалдар бір-біріне паралелль болып орналаспайды, олар өзара бір-бірімен араласқан күйінде болады. Зерттеулер нәтижесінде созылған қабыршықтардың ауданы газ тәрізді қабыршықтар мен конденсацияланған қабыршықтардың ауданының аралығында болатынын дәлелдеген. Созылған қабыршықтардың болуы температура өскен сайын конденсацияланған қабыршықтарда радикалдардың кинетикалық энергиясының көбеюімен түсіндіруге болады. Радикалдардың ұзындығы кішірейген сайын оларға сәйкес оларды конденсациялық қабыршықтардан созылған қабыршыққа айналдыру температурасы да азаяды. Радикалдардың ортасында қос байланыс болғанда созылған қабыршық түзу қабілеті күшейеді. Бұл қос байланыстың суға тағы тартылғандығын көрсетеді. Тәжірибелер беттік қабыршықтардың созылуына молекулардағы полярлы топтың жағдайының әсерлері болатынын көрсетті. Мысалы органикалық қышқылдар белгілі бір температурада бейтараптық және қышқылдық ерітінділерде созылған қабыршықтар түзетін болса, ал сілтілік ерітінділерде қарастырылып отырған жағдай үшін газ тәрізді қабыршықтар береді. Бұл соңғы жағдайда қышқылдардың диссоциациялану нәтижесінде пайда болып, бірдей иондардың тебу нәтижесінде күштердің әсерінен болады.
2.7. БАЗ-дың молекулаларының өлшемін анықтау. Лэнгмюр таразысы Газ тәрізді және конденсацияланған беттік қабыршықтардың болуын Лэнгмюр өзінің арнайы жасаған таразысы арқылы көрсеткен болатын. Бұл таразы арқылы қабыршық болатындай беттік қысымды және оның қабыршықтың ауданымен қандай байланыста болатынын көрсетуге болады. Лэнгмюр таразысының алғашқы түрін сұлбалық түрде 2.5-суреттегідей көрсетуге болады.
Бұндағы 1-бетке дейін толтырылып құйылған ыдыс,2;3 - парафин жұтылған қағаздан жасалған бөгет (тосқауыл). Міне осылардың арасына ұшқыш еріткішке ерітілген судың бетінде беттік қабыршық түзетін заттың ерітіндісін аздап құямыз. Еріткіш оңай ұшып кететіндіктен зат су бетіне жайылып қабыршық түзеді. Сол жаңағы тосқауылды оңға жылжытсақ, онда қабыршық алып тұрған кеңістік кішірейе бастайды. Осының нәтижесінде қабыршықтың беттік қысымы көбейіп, ол 3-ті оңға жылжытады. Сол себепті тепе-теңдікте тұрып таразының күйентесі (4) тепе-теңдіктен ауытқып стрелка басқа бір шаманы көрсетеді. Бастапқы тепе-теңдік жағдайды таразыға ыдысына (5) таразы тастарын салу арқылы келтіріп, қабыршықтың қысымын табуға болады екен. Бұл тәжірибелерді бірнеше рет жасай отырып, қабыршық қысымы мен белгілі бір мөлшердегі зерттеп отырған заттардың ауданының арасындағы изотерманы алуға болады. 2.7 –суретте әртүрлі май қышқылдары үшін 12,5-19,50С-да Адам алған осындай изотермалар көрсетілген. 1-қисық лаурин қышқылына (C11H23COOH) , оның радикалы салыстырмалы түрде қысқалау болғандықтан ол тек газтөрізді беттік қабыршықтар түзеді. Бұл изотерма идеалдық ушөлшемді газдың изотермасын (pV=const)еске түсіреді. Суреттегі 2-қисық миристин қышқылы (C13H27COOH) үшін алынған , ол газтәрізді де, сұйықтәрізді де қабыршықтар түзуге бейім. Бұл жағдайда қабыршықты қысу белгілі-бір дәрежеге жеткенде (бір молекуланың алатын ауданы мен анықталатын ) қысым өспейді де, қисық абцисса осіне параллель болады. Осындай учаскенің болуы екіөлшемдік газдың конденсациялануына және газтәрізді қабыршықтар мен конденсирленген қабыршықтарын «аралшаларының» тепе-теңдігінің болуына сәйкес келеді. Қабыршақты одан ары қысқанда «аралшалар» бір-біріне тығыз жақындап, олардың араасындағы екіөлшемдік газдар болмайды. Сондықтан қысым қайтадан күрт өседі. 3-қисық пальмитин қышқылы C15H31COO бойынша алынған, оның молекулалық масса алғашқы екеуінен жоғары. Бұл қышқылдың радикалдары кәдімгі температураның өзінде күшті әрекеттесетін болғандықтан тек конденсирленген қабыршақтар ғана түзеді. Бұндай қабыршақты едәуір қысқанда қысымның күрт өзгеруі болады. Ол судың барлық беті конденсирленген қабыршықпен жабылғанына сәйкес келеді. Қабыршықты одан әрі қысқанда миристин қышқылында сияқты қабыршықтың бұзылуына әкеп соғады. Беттік қысым мен бір молекуланың алатын ауданының арасындағы тәуелділікті анықтау БАЗ бен түзілетін қабыршақтың табиғатының арасындағы байланысты ғана тауып қоймай, оған қосы қабыршақ құрылысына температураның әсерін де түсіндіруге мүмкіндік береді. Жасалған тәжірибелер температура артқанда алдымен көмірсутектік радикалдар арасындағы молекулалық күштер үзіледі де , қабыршық алдымен созылған қабыршыққа , сосын газтәрізді қабыршыққа айналады. Беттік керілу мен молекулалық аудан арасындағы изотерма бойынша қарастырып отырған затымыздың бір молекуласының бетте алып жатқан ауданын ( S0) табуға болады.
Оны барлық заттың алып тұрған ауданын, оның массасын және молекулалық салмағын біле отырып есептеуге болады.
Бұндағы S0 - 1 моль заттың ауданы; S - қабыршақтың ауданы, ол бөгеулердің ара қашықтығын еніне көбейткенге тең; m - алынған заттың массасы, г бойынша; M - заттың молекулалық салмағы; NА - Авагадро саны. Міне осы айтылған тәсіл бойынша S0 - ды есептеу молекуласында С атомы 14 және одан да көп болатын қаныққан органикалық қышқылдар үшін 20,5 А02 болатынын көрсетті, яғни олардың радикалдарының ұзындығына байланыссыз екен. Бұл БАЗ-дың молекулаларының су бетінде молекулалық қабат пен орналасатынын көрсетеді. Рентгенографиялық зерттеулер кристалдағы бір-біріне өте тығыз орналасатын көмірсутектерінде С атомдарының қимасы 18,4 А02 болатынын көрсетті. Бұл шамалар өте жақын. Бұлардың айырмашылығы иә органикалық қышқылдардағы С орналасуы өте тығыз еместігімен, иә олардың су бетінде тек қана перпендикуляр болып емес, онымен аздап бұрыш жасай орналасатындығымен түсіндіруге болады. Сонымен S0 радикалдарға байланыссыз, ал полярлы топтың табиғатына байланысты екен. Мысалы S0 органикалық қышқылдар үшін - 20,5 А02, күрделі эфирлер үшін - 22 А02, ал спирттер үшін - 21,6 А02 тең екен. Тәжірибелердің нәтижесінде S0-дің беттік табиғатына да байланыссыз екені көрсетілген. Осыған сүйене отырып Гmax және заттың қанша мольінің (n) адсорбцияланған біле отырып, адсорбенттің беттік ауданын есептеп табуға болады. S=nmax/ Гmax Бұл арқылы адсорбенттің меншікті беттік ауданын таба аламыз.
Егер БАЗ бетке перпендикуляр орналасқан деп есептесек, онда қабыршақтың қалыңдығын есептеуге болады. Бірлік аудандағы көлем сол қабыршақтың қалыңдығына тең болады. Басқаша көлемді былай да көрсетуге болады: Гmax Vмоль (Vмоль-мольдік көлем) Ендеше: δ=Гmax Vмоль=ГmaxМ/ρ ρ - тығыздық. Гомологтық қатарда радикалдардың өсуіне байланысты δ өсуі керек. Шындығында да радикал 1 СН2 -топқа өскенде δ 1,43 А0-ге өсетіні тәжірибе арқылы көрсетілген. |
|

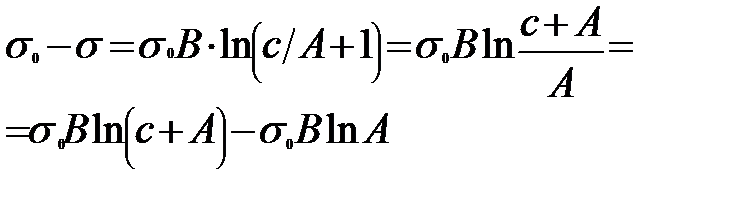
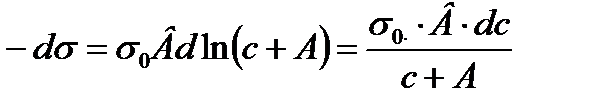
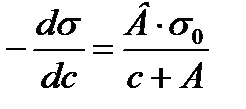
 орнына жоғарғы мәнді қойсақ:
орнына жоғарғы мәнді қойсақ: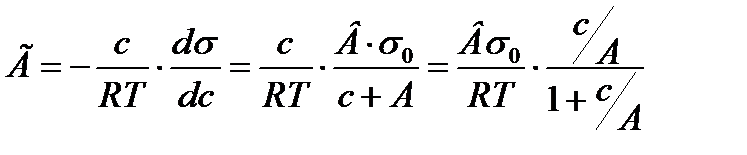
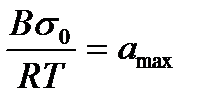
 =
=  =RTln
=RTln 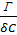
 =RТln3
=RТln3

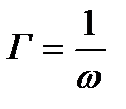
 , немесе ωΔ=RT
, немесе ωΔ=RT 2.5-сурет. Лэнгмюр таразысы.
2.5-сурет. Лэнгмюр таразысы.